题目内容
【题目】已知函数y=f(x)和y=g(x)在[-2,2]上的图象如图所示.给出下列四个命题:
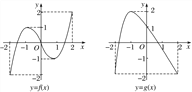
①方程f[g(x)]=0有且仅有6个根;②方程g[f(x)]=0有且仅有3个根;
③方程f[f(x)]=0有且仅有7个根;④方程g[g(x)]=0有且仅有4个根.
其中正确命题的序号为________.
【答案】①④
【解析】①设t=g(x),则由f[g(x)]=0,得f(t)=0,则t1=0或-2<t2<-1或1<t3<2.当t1=0时,g(x)=0有2个不同根;当-2<t2<-1时,g(x)=t2有2个不同根;当1<t3<2时,g(x)=t3有2个不同根,∴方程f[g(x)]=0有且仅有6个根,故①正确.
②设t=f(x),若g[f(x)]=0,则g(t)=0,则-2<t1<-1或0<t2<1.当-2<t1<-1时,f(x)=t1有1个根;当0<t2<1时,f(x)=t2有3个不同根,
∴方程g[f(x)]=0有且仅有4个根,故②错误.
③设t=f(x),若f[f(x)]=0,则f(t)=0,则t1=0或-2<t2<-1或1<t3<2.当t1=0时,f(x)=t1有3个不同根;当-2<t2<-1时,f(x)=t2有1个根;当1<t3<2时,f(x)=t3有1个根,∴方程f[f(x)]=0有且仅有5个根,故③错误.
④设t=g(x),若g[g(x)]=0,则g(t)=0,则-2<t1<-1或0<t2<1.当-2<t1<-1时,g(x)=t1有2个不同根;当0<t2<1时,g(x)=t2有2个不同根,∴方程g[g(x)]=0有且仅有4个根,故④正确.
综上,命题①④正确.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目