题目内容
一个口袋中有 个白球和
个白球和 个红球(
个红球(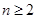 ,且
,且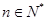 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;
(2)若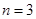 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为 ,当
,当 为何值时,
为何值时, 取最大值.
取最大值.
 个白球和
个白球和 个红球(
个红球(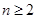 ,且
,且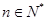 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.(1)试用含
 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率 ;
;(2)若
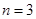 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;(3)记三次摸球恰有一次中奖的概率为
 ,当
,当 为何值时,
为何值时, 取最大值.
取最大值.(1) ,(2)
,(2)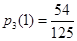 ,(3)
,(3) 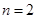 .
.
 ,(2)
,(2)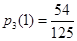 ,(3)
,(3) 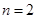 .
.试题分析:(1)求古典概型概率,关键正确计算事件所包含的基本事件. 一次摸球从
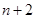 个球中任选两个,有
个球中任选两个,有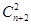 种选法,其中两球颜色相同有
种选法,其中两球颜色相同有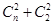 种选法;因此一次摸球中奖的概率
种选法;因此一次摸球中奖的概率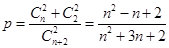 .(2)因为每次摸球后把这两个球放回袋中,所以事件为独立重复试验. 由(1)得一次摸球中奖的概率是
.(2)因为每次摸球后把这两个球放回袋中,所以事件为独立重复试验. 由(1)得一次摸球中奖的概率是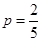 ,所以三次摸球恰有一次中奖的概率是
,所以三次摸球恰有一次中奖的概率是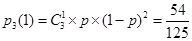 .(3)同(2)可得三次摸球中恰有一次中奖的概率是
.(3)同(2)可得三次摸球中恰有一次中奖的概率是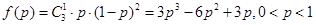 ,这是三次函数,利用导数求最值. 由
,这是三次函数,利用导数求最值. 由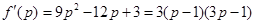 知
知 在
在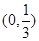 是增函数,在
是增函数,在 是减函数,所以当
是减函数,所以当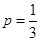 时,
时, 取最大值.
取最大值.试题解析:(1)一次摸球从
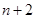 个球中任选两个,有
个球中任选两个,有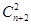 种选法,
种选法,其中两球颜色相同有
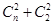 种选法;
种选法; ∴一次摸球中奖的概率
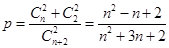 . 4分
. 4分(2)若
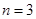 ,则一次摸球中奖的概率是
,则一次摸球中奖的概率是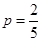 ,三次摸球是独立重复实验,三次摸球中恰有一次中奖的概率是
,三次摸球是独立重复实验,三次摸球中恰有一次中奖的概率是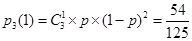 . 8分
. 8分(3)设一次摸球中奖的概率是
 ,
,则三次摸球中恰有一次中奖的概率是
 ,
,∵
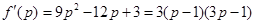 ,
,∴
 在
在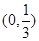 是增函数,在
是增函数,在 是减函数,
是减函数,∴当
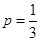 时,
时, 取最大值. 10分
取最大值. 10分由
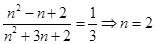 .
.∴
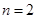 时,三次摸球中恰有一次中奖的概率最大. 12分
时,三次摸球中恰有一次中奖的概率最大. 12分
练习册系列答案
相关题目
 的概率.
的概率. 满足
满足 ,则
,则



 有实根的概率为( )
有实根的概率为( )