题目内容
(1)已知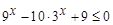 ,求函数
,求函数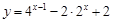 的最大值和最小值;
的最大值和最小值;
(2)要使函数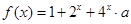 在
在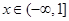 上f (x)
上f (x)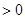 恒成立,求a的取值范围.
恒成立,求a的取值范围.
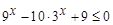 ,求函数
,求函数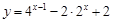 的最大值和最小值;
的最大值和最小值;(2)要使函数
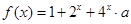 在
在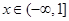 上f (x)
上f (x)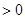 恒成立,求a的取值范围.
恒成立,求a的取值范围.(1)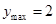 ,
,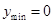 ;(2)
;(2)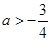
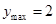 ,
,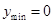 ;(2)
;(2)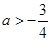
试题分析:(1)由
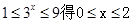 2分
2分令
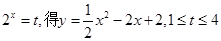 3分
3分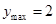 5分
5分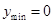 7分
7分(2)分离参数得
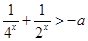 9分
9分换元得:
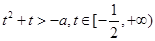 11分
11分得:
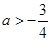 14分
14分点评:利用函数的单调性确定其值域是高考热点,关键在于发现函数的单调性

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 是增函数,且函数
是增函数,且函数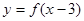 的图像关于(3,0)成中心对称,若
的图像关于(3,0)成中心对称,若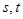 满足不等式
满足不等式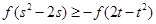 ,当
,当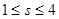 时,则
时,则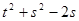 的取值范围为____.
的取值范围为____. 的最大允许值是多少?
的最大允许值是多少? .
. 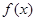 的图像关于点
的图像关于点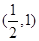 对称;
对称;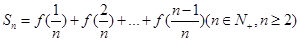 ,求
,求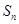 ;
;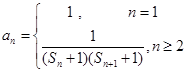
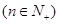 ,
,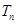 为数列
为数列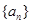 的前
的前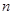 项和,若
项和,若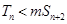 对一切
对一切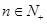 都成立,试求实数
都成立,试求实数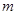 的取值范围.
的取值范围.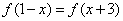 ,且
,且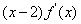 <0a="f" (
<0a="f" (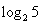 ),b="f" (
),b="f" (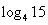 ),c="f" (
),c="f" (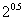 ),则a,b,c的大小关系为
),则a,b,c的大小关系为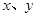 的二元一次方程组
的二元一次方程组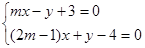 有唯一一组解,则实数
有唯一一组解,则实数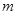 的取值范围是
的取值范围是 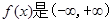 上的奇函数,且
上的奇函数,且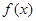 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当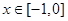 时,
时,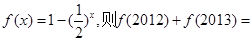 .
.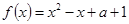
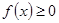 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。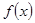 在区间
在区间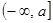 上的最小值
上的最小值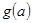 的表达式。
的表达式。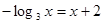 的根所在的区间为 ( )
的根所在的区间为 ( )