题目内容
以双曲线
的上焦点为圆心，与该双曲线的渐近线相切的圆的方程为 .
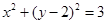
解析试题分析：由题意知，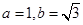
，则
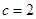，上焦点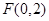
为圆心，而F到渐近线距离=
，
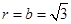所以圆为.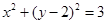
考点：双曲线的标准方程、圆的标准方程.
练习册系列答案
相关题目
题目内容
以双曲线的上焦点为圆心，与该双曲线的渐近线相切的圆的方程为 .
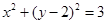
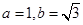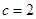解析试题分析：由题意知，，则，上焦点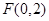为圆心，而F到渐近线距离=，
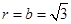所以圆为.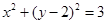
考点：双曲线的标准方程、圆的标准方程.
＝－2y2的准线方程是 .
的右焦点与抛物线
的焦点重合，则该双曲线的焦点到其渐近线的距离为 。
的正方体
中，点
是正方体棱上一点（不包括棱的端点），
，
，则满足条件的点
，则
的取值范围是________．
与圆x2+y2=a2+b2在第一象限的交点，其中F1,F2分别是双曲线的左、右焦点，且
，则双曲线的离心率为______.[来
是双曲线
的右焦点，点
、
分别在其两条渐近线上，且满足
，
（
为坐标原点），则该双曲线的离心率为____________.
＝1的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则
·
的最小值为________．