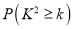题目内容
【题目】从某小学的期末考试中抽取部分学生的数学成绩，由抽查结果得到如图的频率分布直方图，分数落在区间
，
，
内的频率之比为
．
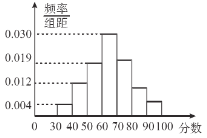
（1）求这些学生的分数落在区间内的频率；
（2）（ⅰ）若采用分层抽样的方法从分数落在区间
，
内抽取4人，求从分数落在区间，内各抽取的人数；
（ⅱ）从上述抽取的4人中再随机抽取2人，求这2人全部来自于区间内的概率．
【答案】（1）
；（2）（ⅰ）从分数落在区间
，
内各抽取的人数为
； （ⅱ）
．
【解析】
（1）设区间
内的频率为
，则区间
，
内的频率分别为
和
，然后利用所有矩形的面积和为1建立方程求解即可
（2）（ⅰ）算出区间
内的频率与区间
内的频率之比即可
（ⅱ）落在区间内的1人为
，落在区间内的3人为
，
，
，列出所有的情况和满足所求事件的情况即可.
（1）设区间内的频率为，
则区间，内的频率分别为和．
依题意得
，解得
．
所以区间内的频率为．
（2）（ⅰ）区间内的频率与区间内的频率之比为
，
所以从分数落在区间，内各抽取的人数为
，
．
（ⅱ）记上述抽取的4人中，落在区间内的1人为，落在区间内的3人为，，，
从上述抽取的4人中再随机抽取2人，其所有情况有
，
，
，
，
，
，共6种，
其中这2人全部来自区间内的情况有3种，
所以这2人全部来自于区间内的概率
【题目】某家政公司对部分员工的服务进行民意调查，调查按各项服务标准进行量化评分，婴幼儿保姆部对40～50岁和20～30岁各20名女保姆的调查结果如下：
分数 年龄 |
|
|
|
|
|
40～50岁 | 0 | 2 | 4 | 7 | 7 |
20～30岁 | 3 | 5 | 5 | 5 | 2 |
（1）若规定评分不低于80分为优秀保姆，试分别估计这两个年龄段保姆的优秀率；
（2）按照大于或等于80分为优秀保姆，80分以下为非优秀保姆统计.作出
列联表，并判断能否有
的把握认为对保姆工作质量的评价是否优秀与年龄有关.
（3）从所有成绩在70分以上的人中按年龄利用分层抽样抽取10名保姆，再从这10人中选取3人给大家作经验报告，设抽到40～50岁的保姆的人数为
，求出的分布列与期望值.
下面的临界值表供参考：
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：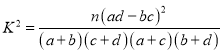
，其中
.