题目内容
某灯管厂生产的新型节能灯管的使用寿命(使用时间:小时)为随机变量Y,已知Y~N(1000,302),要使灯管的平均寿命为1000小时的概率为99.74%,问灯管的最低寿命应控制在多少小时以上?
应控制在910小时以上.
解:因为 ,又Y~N(1000,302), 所以Y在(910,1090)内取值的概率为99.74%,故最低寿命应控制在910小时以上.
,又Y~N(1000,302), 所以Y在(910,1090)内取值的概率为99.74%,故最低寿命应控制在910小时以上.
 ,又Y~N(1000,302), 所以Y在(910,1090)内取值的概率为99.74%,故最低寿命应控制在910小时以上.
,又Y~N(1000,302), 所以Y在(910,1090)内取值的概率为99.74%,故最低寿命应控制在910小时以上.
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 ,求总体位于区间[-4,-2]的概率.
,求总体位于区间[-4,-2]的概率. ,
, ),且EX=3,DX=1,则P(-1<X<1)="( " )
),且EX=3,DX=1,则P(-1<X<1)="( " )
 曲线
曲线 ( )
( )

 与
与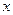 轴相交
轴相交
 分别与
分别与