题目内容
函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
| A.(-1,1) | B.(-1,+∞) |
| C.(-∞,-1) | D.(-∞,+∞) |
B
解析

练习册系列答案
相关题目
已知函数 在
在 上的最大值为
上的最大值为 ,则函数
,则函数
的零点的个数为( )
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使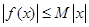 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:①
为“倍约束函数”,现给出下列函数:① :②
:②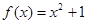 :③
:③ ;④
;④ ⑤
⑤ 是定义在实数集R上的奇函数,且
是定义在实数集R上的奇函数,且
对一切 均有
均有 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.[1,+∞) |
| C.(0,1] | D.(0,1) |
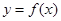 在区间
在区间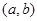 上的导函数为
上的导函数为 ,
,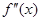 ,若在区间
,若在区间 恒成立,则称函数
恒成立,则称函数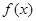 在区间
在区间 ,若对任意的实数
,若对任意的实数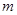 满足
满足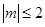 时,函数
时,函数 的最大值为( )
的最大值为( ) ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( )


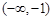

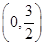 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( ) ﹣1的图象大致是( )
﹣1的图象大致是( )



 为
为  的导函数,则
的导函数,则  的图象大致是( )
的图象大致是( )