题目内容
【题目】已知椭圆![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且当点
两点,且当点![]() 是椭圆
是椭圆![]() 的上顶点时,
的上顶点时,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若
,若![]() ,求此时
,求此时![]() 的方程.
的方程.

【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意可以知![]() ,可求出点
,可求出点![]() 的坐标,又点
的坐标,又点![]() 在椭圆
在椭圆![]() 上,将点
上,将点![]() 的坐标代入椭圆方程,即可求出
的坐标代入椭圆方程,即可求出![]() ,进而求出椭圆方程;
,进而求出椭圆方程;
(2)当直线![]() 与垂直或与
与垂直或与![]() 轴重合时,不满足题意,故可设直线
轴重合时,不满足题意,故可设直线![]() 方程为:
方程为:![]() ,由
,由![]() 可知四边形
可知四边形![]() 为平行四边形,可得点
为平行四边形,可得点![]() 为线段
为线段![]() 的中点,再根据点差法即可求出结果.
的中点,再根据点差法即可求出结果.
(1)由题意可以知![]() ,
,![]() 、
、![]() ,设
,设![]()
则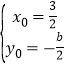
∵点![]() 在椭圆
在椭圆![]() 上 ∴
上 ∴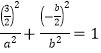 解得
解得![]()
∴![]() ∴椭圆
∴椭圆![]() 的方程为:
的方程为:![]()
(2)当直线![]() 与垂直或与
与垂直或与![]() 轴重合时,不满足题意
轴重合时,不满足题意
∴可直线![]() 方程为:
方程为:![]()
设![]() 、
、![]() 、
、![]() 、
、![]()
由![]() 可知四边形
可知四边形![]() 为平行四边形
为平行四边形
∴点![]() 为线段
为线段![]() 的中点
的中点
由![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 、
、![]() 在椭圆
在椭圆![]() 上
上
∴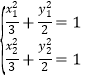 则
则![]()
可得![]() 又∵
又∵![]()
可解得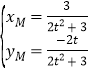 ∴
∴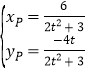
∵点![]() 在椭圆
在椭圆![]() 上
上
∴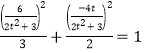 整理得
整理得![]()
解得![]() 或
或![]() 舍去
舍去
∴![]() 可知
可知![]() 的方程为
的方程为![]() 即
即![]() .
.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
【题目】2019年以来,我国国内非洲猪瘟疫情严重,引发猪肉价格上涨.因此,国家为保民生采取宏观调控对猪肉价格进行有效地控制.通过市场调查,得到猪肉价格在近四个月的市场平均价![]() (单位:元/斤)与时间
(单位:元/斤)与时间![]() (单位:月)的数据如下:( )
(单位:月)的数据如下:( )
| 8 | 9 | 10 | 11 |
| 28.00 | 33.99 | 36.00 | 34.02 |
现有三种函数模型:![]() ,
,![]() ,
,![]() ,找出你认为最适合的函数模型,并估计2019年12月份的猪肉市场平均价为( )
,找出你认为最适合的函数模型,并估计2019年12月份的猪肉市场平均价为( )
A.28B.25C.23D.21


