Question

【题目】将函数y＝sin2x－cos2x的图象向左平移m（m＞0）个单位以后得到的图象与函数y＝ksinxcosx（k＞0）的图象关于（，0）对称，则k＋m的最小正值是

A. 2＋ B. 2＋ C. 2＋ D. 2＋

Answer 1

【答案】C

【解析】

由题意可得y=﹣cos（2x﹣2m）的图象和y=sin2x（k＞0）的图象关于点对称，设点

P（x0，y0）为y=﹣cos（2x﹣2m）上任意一点，则该点关于对称点为在

y=sin2x（k＞0）的图象上，故有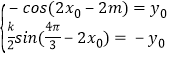，求得k=2，且cos（2x0﹣）=cos

（2x0﹣2m），由此求得k+m的最小正值．

将函数y=sin2x﹣cos2x=﹣cos2x的函数图象向右平移m个单位以后得到y=﹣cos2（x﹣m）=

﹣cos（2x﹣2m）的图象，

根据所得图象与y=ksinxcosx=sin2x（k＞0）的图象关于对称，

设点P（x0，y0）为y=﹣cos（2x﹣2m）上任意一点，

则该点关于对称点为在y=sin2x（k＞0）的图象上，故有

，

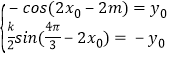所以k=2，sin（2x0﹣）=cos（2x0﹣2m），即cos（2x0﹣）=cos（2x0﹣2m），

∴﹣2m=﹣+2kπ，k∈Z，即 2m=﹣2kπ，k∈Z，故m的最小正值为，

则k+m的最小正值为2+．故答案为：C