Question

【题目】已知直线l1：y＝x，l2：y＝－x，动点P，Q分别在l1，l2上移动，｜PQ｜＝2，N是线段PQ的中点，记点N的轨迹为曲线C．

（Ⅰ）求曲线C的方程；

（Ⅱ）过点M（0，1）分别作直线MA，MB交曲线C于A，B两点，设这两条直线的斜率分别为k1，k2，且k1＋k2＝2，证明：直线AB过定点．

Answer 1

【答案】（1） ； （2）（-1，-1）.

【解析】

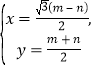（Ⅰ）根据条件设P，Q，由得，设N（x，y）是线段PQ的中点，所以 消去m，n可得曲线C的方程. （Ⅱ）先求出直线AB的方程，再找到定点.

（Ⅰ）根据条件设P，Q，∵，

即，∵N（x，y）是线段PQ的中点，∴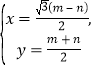

消去m，n可得曲线C的方程为.

（Ⅱ）由（Ⅰ）知，点M（0，1）为椭圆的上顶点，

当直线AB的斜率不存在时，设A，则B，

由得，得；

当直线AB的斜率存在时，设AB的方程为、A， B，

，得，

，

即，

由m≠1，，

即，故直线AB过定点（-1，-1）.

经检验，此时直线与椭圆有两个交点，满足题意.综上所述，直线AB过定点（-1，-1）.