题目内容
设a>0,b>0,a+b=1.
(1)试比较a2+b2与ab的大小;
(2)证明:ab+ ≥
≥ .
.
解:(1)∵a>0,b>0
∴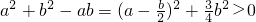
∴a2+b2>ab.
(2)证明:ab+ ≥4
≥4 ?4a2b2-17ab+4≥0
?4a2b2-17ab+4≥0
??(4ab-1)( ab-4)≥0.
∵ab=( )2≤
)2≤ =
= ,
,
∴4ab≤1,
而又∵a+b=1
∴ab≤ <4,
<4,
因此(4ab-1)(ab-4)≥0成立,故ab+ ≥4
≥4 .
.
分析:(1)用作差法比较两个数的大小,先做差,再对所得的差配方得出差的符号,即可判断出两式的大小;
(2)先将不等式转化为ab+ ≥4
≥4 ?4a2b2-17ab+4≥0然后再整理成两个因子的乘积即ab+
?4a2b2-17ab+4≥0然后再整理成两个因子的乘积即ab+ ≥4
≥4 ?(4ab-1)( ab-4)≥0,由此判断知需要先研究ab的取值范围,再判断(4ab-1)( ab-4)≥0成立,即可证明不等式
?(4ab-1)( ab-4)≥0,由此判断知需要先研究ab的取值范围,再判断(4ab-1)( ab-4)≥0成立,即可证明不等式
点评:本题考查不等式的证明与大小比较,解题的关键是掌握不等式的证明方法比较法,及等价转化的技巧,不等式证明最基本的访求即为比较法,现在的高中教材对不等式的证明基本上就是要求掌握住比较法,综合法,分析法,不等式证明的难度与要求大降低,对基本的证明方法要认真研究其规律,娴熟运用.
∴
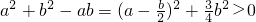
∴a2+b2>ab.
(2)证明:ab+
 ≥4
≥4 ?4a2b2-17ab+4≥0
?4a2b2-17ab+4≥0??(4ab-1)( ab-4)≥0.
∵ab=(
 )2≤
)2≤ =
= ,
,∴4ab≤1,
而又∵a+b=1
∴ab≤
 <4,
<4,因此(4ab-1)(ab-4)≥0成立,故ab+
 ≥4
≥4 .
.分析:(1)用作差法比较两个数的大小,先做差,再对所得的差配方得出差的符号,即可判断出两式的大小;
(2)先将不等式转化为ab+
 ≥4
≥4 ?4a2b2-17ab+4≥0然后再整理成两个因子的乘积即ab+
?4a2b2-17ab+4≥0然后再整理成两个因子的乘积即ab+ ≥4
≥4 ?(4ab-1)( ab-4)≥0,由此判断知需要先研究ab的取值范围,再判断(4ab-1)( ab-4)≥0成立,即可证明不等式
?(4ab-1)( ab-4)≥0,由此判断知需要先研究ab的取值范围,再判断(4ab-1)( ab-4)≥0成立,即可证明不等式点评:本题考查不等式的证明与大小比较,解题的关键是掌握不等式的证明方法比较法,及等价转化的技巧,不等式证明最基本的访求即为比较法,现在的高中教材对不等式的证明基本上就是要求掌握住比较法,综合法,分析法,不等式证明的难度与要求大降低,对基本的证明方法要认真研究其规律,娴熟运用.

练习册系列答案
相关题目
设a>0,b>0,a+b+ab=24,则( )
| A、a+b有最大值8 | B、a+b有最小值8 | C、ab有最大值8 | D、ab有最小值8 |