题目内容
在R上定义运算⊕:x⊕y=x(1-y),若不等式(x-1)⊕(x+2)<0,则实数x的取值范围是( )
分析:由题目给出的新定义,把不等式(x-1)⊕(x+2)<0转化为(x-1)(1-x-2)<0,然后直接求解一元二次不等式即可得到x的取值范围.
解答:解:由定义x⊕y=x(1-y)知,(x-1)⊕(x+2)=(x-1)(1-x-2),
所以,不等式(x-1)⊕(x+2)<0转化为(x-1)(1-x-2)<0,
即(x-1)(x+1)>0,解得:x<-1或x>1.
所以不等式(x-1)⊕(x+2)<0的解集为{x|x<-1或x>1}.
故选C.
所以,不等式(x-1)⊕(x+2)<0转化为(x-1)(1-x-2)<0,
即(x-1)(x+1)>0,解得:x<-1或x>1.
所以不等式(x-1)⊕(x+2)<0的解集为{x|x<-1或x>1}.
故选C.
点评:本题考查了新定义,考查了一元二次不等式的解法,是基础的运算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 :x
:x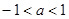 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.