题目内容
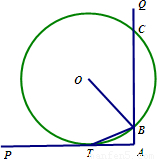
 (1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA
(1)如图,∠PAQ是直角,圆O与AP相切于点T,与AQ相交于两点B,C.求证:BT平分∠OBA(2)若点A(2,2)在矩阵M=
|
(3)在极坐标系中,A为曲线ρ2+2ρcosθ-3=0上的动点,B为直线ρcosθ+ρsinθ-7=0上的动点,求AB的最小值;
(4)已知a1,a2…an都是正数,且a1•a2…an=1,求证:(2+a1)(2+a2)…(2+an)≥3n.
分析:(1)证明BT平分∠OBA,即证明∠OBT=∠TBA,利用∠TBA=∠BTO,∠OTB=∠OBT,可得结论;
(2)根据点A(2,2)在矩阵M=
对应变换的作用下得到的点为B(-2,2),建立方程,求得M,再利用M-1=
,可得矩阵M的逆矩阵,或利用矩阵M的行列式,求得矩阵M的逆矩阵;
(3)将圆、直线的极坐标方程化为直角坐标方程方程,求出圆心到直线的距离d=
=4
,即可求AB的最小值;
(4)因为a1是正数,所以2a1=1+1+a1≥3
,同理,2aj≥1+1+aj≥3
,将上述不等式两边相乘,利用a1•a2•…•an=1,即可证得结论.
(2)根据点A(2,2)在矩阵M=
|
|
(3)将圆、直线的极坐标方程化为直角坐标方程方程,求出圆心到直线的距离d=
| |-1-7| | ||
|
| 2 |
(4)因为a1是正数,所以2a1=1+1+a1≥3
| 3 | a |
| 3 | aj |
解答: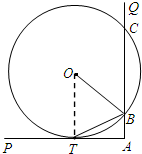 (1)证明:连接OT,因为AT是切线,所以OT⊥AP.
(1)证明:连接OT,因为AT是切线,所以OT⊥AP.
因为∠PAQ是直角,即AQ⊥AP,所以AB∥OT,所以∠TBA=∠BTO.(5分)
因为OT=OB,所以∠OTB=∠OBT,
所以∠OBT=∠TBA,
即BT平分∠OBA.(10分)
(2)解:由题意知,M
=
,即
=
,
所以
,解得
所以M=
.(5分)
由M-1M=
,解得M-1=
.(10分)
另解:矩阵M的行列式|M|=
=1≠0,所以M-1=
.
(3)解:圆方程为(x+1)2+y2=4,圆心(-1,0),直线方程为x+y-7=0,(5分)
圆心到直线的距离d=
=4
,所以(AB)min=4
-2. (10分)
(4)证明:因为a1是正数,所以2a1=1+1+a1≥3
,(5分)
同理,2aj≥1+1+aj≥3
,
将上述不等式两边相乘,得(2+a1)(2+a2)…(2+an)≥3n•
,
因为a1•a2•…•an=1,所以(2+a1)(2+a2)…(2+an)≥3n.(10分)
 (1)证明:连接OT,因为AT是切线,所以OT⊥AP.
(1)证明:连接OT,因为AT是切线,所以OT⊥AP.因为∠PAQ是直角,即AQ⊥AP,所以AB∥OT,所以∠TBA=∠BTO.(5分)
因为OT=OB,所以∠OTB=∠OBT,
所以∠OBT=∠TBA,
即BT平分∠OBA.(10分)
(2)解:由题意知,M
|
|
|
|
所以
|
|
所以M=
|
由M-1M=
|
|
另解:矩阵M的行列式|M|=
|
|
(3)解:圆方程为(x+1)2+y2=4,圆心(-1,0),直线方程为x+y-7=0,(5分)
圆心到直线的距离d=
| |-1-7| | ||
|
| 2 |
| 2 |
(4)证明:因为a1是正数,所以2a1=1+1+a1≥3
| 3 | a |
同理,2aj≥1+1+aj≥3
| 3 | aj |
将上述不等式两边相乘,得(2+a1)(2+a2)…(2+an)≥3n•
| 3 | a1•a2•…•an |
因为a1•a2•…•an=1,所以(2+a1)(2+a2)…(2+an)≥3n.(10分)
点评:本题考查几何证明选讲,考查矩阵与变换,考查极坐标方程,考查不等式的证明,涉及知识点多,综合性强.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答, (2012•江苏一模)选修4-1:几何证明选讲
(2012•江苏一模)选修4-1:几何证明选讲 (几何证明选做题)如图,∠PAQ是直角,半径为5的圆O与AP相切于点T,与AQ相交于两点B、C,BT是否平分∠OBA?证明你的结论;
(几何证明选做题)如图,∠PAQ是直角,半径为5的圆O与AP相切于点T,与AQ相交于两点B、C,BT是否平分∠OBA?证明你的结论;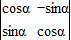 对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵;
对应变换的作用下得到的点为B(-2,2),求矩阵M的逆矩阵; .
.