Question

本题包括（1）、（2）、（3）、（4）四小题，请选定其中两题，并在答题卡指定区域内答，
若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．
（1）、选修4-1：几何证明选讲
如图，∠PAQ是直角，圆O与AP相切于点T，与AQ相交于两点B，C．求证：BT平分∠OBA
（2）选修4-2：矩阵与变换（本小题满分10分）
若点A（2，2）在矩阵M=

cosα -sinα sinα cosα

对应变换的作用下得到的点为B（-2，2），求矩阵M的逆矩阵
（3）选修4-2：矩阵与变换（本小题满分10分）
在极坐标系中，A为曲线ρ²+2ρcosθ-3=0上的动点，B为直线ρcosθ+ρsinθ-7=0上的动点，求AB的最小值．
（4）选修4-5：不等式选讲（本小题满分10分）
已知a₁，a₂…a_n都是正数，且a₁•a₂…a_n=1，求证：（2+a₁）（2+a₂）…（2+a_n）≥3ⁿ．

Answer 1

分析：（1）要证明BT平分∠OBA，即证∠OBT=∠ABT，根据∠PAQ是直角，圆O与AP相切于点T，联想到切线的性质，我们可以先连接OT，然后根据QA∥OT，结合角与角之间的等量代换，我们易得结论．
（2）首先由点A（2，2）在矩阵M对应变换作用下得到的点为B（-2，2）以及矩阵M的参数表达式可以解除矩阵M，再根据M^-1M=E，可直接解出矩阵M的逆矩阵．
（3）先将ρ²+2ρcosθ-3=0和直线ρcosθ+ρsinθ-7=0极坐标方程利用直角坐标与极坐标间的关系，即利用ρcosθ=x，ρsinθ=y，ρ²=x²+y²，进行代换即得直角坐标方程．再利用点到直线的距离求得|AB|距离的最小值即可．
（4）根据不等式的结构特征，得出2+a_n=1+1+a_n≥3•

3	an

＞0，对各项放缩后，再利用不等式的性质同向不等式相乘．

解答：（1）证明：连接OT，
∵AT是切线，
∴OT⊥AP．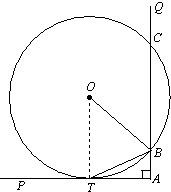
又∵∠PAB是直角，即AQ⊥AP
∴AB∥OT，
∴∠TBA=∠BTO
又∵OT=OB，
∴∠OTB=∠OBT．
∴∠OBT=∠TBA，即BT平分∠OBA
（2）解：因为点A（2，2）在矩阵M对应变换作用下得到的点为B（-2，2），
故有：M

2 2

=

-2 2

，即

2cosα-2sinα 2sinα+2cosα

=

-2 2

，
所以cosα-sinα=-1，cosα+sinα=1，
可解得：cosα=0，sinα=1，
所以M=

0 -1 1 0

，由M^-1M=

1 0 0 1

，
可解得矩阵M的逆矩阵M-1=

0 1 -1 0

．
（3）解：圆方程为（x+1）²+y²=4，圆心（-1，0），直线方程为x+y-7=0
圆心到直线的距离d=

|-1-7|

2

=4

2

，所以|AB|_min=4

2

-2．
（4）证明：∵a₁＞0，1＞0；
∴2+a₁=1+1+a₁≥≥3•

3	a1

＞0；…（2分）
同理：2+a₂=1+1+a₂≥3•

3	a2

＞0；…，2+a_n=1+1+a_n≥

3	an

＞0
由不等式性质：上面n大于0的同向不等式相乘，即得：（2+a₁）（2+a₂）…（2+a_n）≥3ⁿ•

3	a1a2…an

…（4分）
∵已知：a₁•a₂…a_n=1，代入上式得：（2+a₁）（2+a₂）…（2+a_n）≥3ⁿ…（6分）

点评：本题是选做题，考查四方面的内容，主要考查二阶矩阵变化以及由矩阵求其逆矩阵的方法，考查点的极坐标和直角坐标的互化，考查不等式的证明，用到了利用三元均值不等式放缩法和不等式的性质．