题目内容
一元二次方程
有一个正根和一个负根的充分不必要条件是
| A．a<0 | B．a>0 | C．a<-1 | D．a>1 |
C
解析试题分析：方程有一个正根和一个负根，则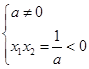
，解得a<0。所以一元二次方程有一个正根和一个负根的充分不必要条件是<-1。故选C。
考点：充分条件与必要条件
点评：判断两个条件之间的关系是一个重要的考点。本题就是结合结论：
若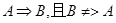
，则A是B的充分而不必要条件。
练习册系列答案
相关题目
下列四个命题中，正确的是（ ）
A．已知 服从正态分布 ，且 ，则 |
B．已知命题 ;命题 ．则命题“ ”是假命题 |
C．设回归直线方程为 ，当变量 增加一个单位时， 平均增加2个单位 |
D．已知直线 , ，则 的充要条件是 =-3 |
下面四个条件中，使
成立的充分而不必要的条件是( )
A． | B． | C． | D． |
命题“所有能被2整除的整数都是偶数”的否定是 （ ）
| A．所有不能被2整除的整数都是偶数 | B．所有能被2整除的整数都不是偶数 |
| C．存在一个不能被2整除的整数是偶数 | D．存在一个能被2整除的整数不是偶数 |
下列命题正确的是
A． | B． |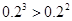
C． | D．  |
给出下面四个命题：
（1）如果直线
，那么
可以确定一个平面；（2）如果直线
和
都与直线
相交，那么可以确定一个平面；（3）如果
那么可以确定一个平面；（4）直线过平面
内一点与平面外一点，直线在平面内不经过该点，那么和是异面直线。上述命题中，真命题的个数是（ ）
| A．1个； | B．2个； | C．3个； | D．4个。 |
下列说法中，错误的是 （ ）
A． |
B．若 的逆否命题为真命题 |
C．命题 |
D．若 |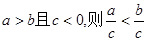
已知a，b，c∈R，命题“若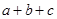
=3，则
≥3”的否命题是（ ）
| A．若a+b+c≠3，则<3 | B．若a+b+c=3，则<3 |
| C．若a+b+c≠3，则≥3 | D．若≥3，则a+b+c=3 |
给定两个命题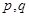
，
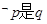的必要而不充分条件，则
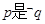的( )
| A．充分而不必要条件 | B．必要而不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |