题目内容
已知椭圆 ,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )
,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )A.1
B.2
C.3
D.4
【答案】分析:根据椭圆的定义,得到|MF1|+|MF2|=10,根据点M到左焦点F1的距离为2,得到|MF2|=10-2=8,最后在△MF1F2中,利用中位线定理,得到|ON|的值.
解答:解:∵椭圆方程为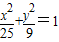 ,
,
∴椭圆的a=5,长轴2a=10,可得椭圆上任意一点到两个焦点F1、F2距离之和等于10.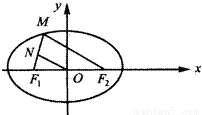
∴|MF1|+|MF2|=10
∵点M到左焦点F1的距离为2,即|MF1|=2,
∴|MF2|=10-2=8,
∵△MF1F2中,N、O分别是MF1、F1F2中点
∴|ON|= |MF2|=4.
|MF2|=4.
故选D.
点评:本题考查了三角形中位线定理和椭圆的定义等知识点,考查学生的计算能力,属于基础题.
解答:解:∵椭圆方程为
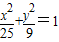 ,
,∴椭圆的a=5,长轴2a=10,可得椭圆上任意一点到两个焦点F1、F2距离之和等于10.

∴|MF1|+|MF2|=10
∵点M到左焦点F1的距离为2,即|MF1|=2,
∴|MF2|=10-2=8,
∵△MF1F2中,N、O分别是MF1、F1F2中点
∴|ON|=
 |MF2|=4.
|MF2|=4.故选D.
点评:本题考查了三角形中位线定理和椭圆的定义等知识点,考查学生的计算能力,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
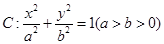 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点,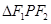 的重心为G,内心I,且有
的重心为G,内心I,且有 (其中
(其中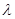 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )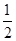 B.
B.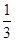 C.
C.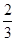 D.
D.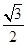
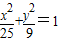 ,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )
,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )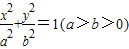 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .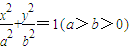 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .