题目内容
已知椭圆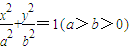 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
【答案】分析:设点P到直线l的距离为d,根据椭圆的定义可知|PF2|比d的值等于c比a的值,由题意知|PF1|等于2d,且|PF1|+|PF2|=2a,联立化简得到:|PF1|等于一个关于a与c的关系式,又|PF1|大于等于a-c,小于等于a+c,列出关于a与c的不等式,求出不等式的解集即可得到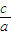 的范围,即为离心率e的范围,同时考虑e小于1,从而得到此椭圆离心率的范围.
的范围,即为离心率e的范围,同时考虑e小于1,从而得到此椭圆离心率的范围.
解答:解:设P到直线l的距离为d,
根据椭圆的第二定义得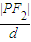 =e=
=e= ,|PF1|=2d,且|PF1|+|PF2|=2a,
,|PF1|=2d,且|PF1|+|PF2|=2a,
则|PF1|=2a-|PF2|=2a-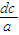 =2d,即d=
=2d,即d=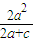 ,
,
而|PF1|∈(a-c,a+c),即2d=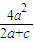 ,
,
所以得到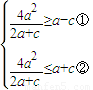 ,由①得:
,由①得: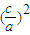 +
+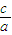 +2≥0,
+2≥0,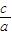 为任意实数;
为任意实数;
由②得: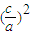 +3
+3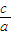 -2≥0,解得
-2≥0,解得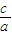 ≥
≥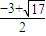 或
或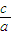 ≤
≤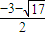 (舍去),
(舍去),
所以不等式的解集为: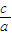 ≥
≥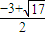 ,即离心率e≥
,即离心率e≥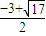 ,又e<1,
,又e<1,
所以椭圆离心率的取值范围是[ ,1).
,1).
故答案为:[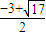 ,1)
,1)
点评:此题考查学生掌握椭圆的定义及椭圆简单性质的运用,是一道中档题.
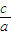 的范围,即为离心率e的范围,同时考虑e小于1,从而得到此椭圆离心率的范围.
的范围,即为离心率e的范围,同时考虑e小于1,从而得到此椭圆离心率的范围.解答:解:设P到直线l的距离为d,
根据椭圆的第二定义得
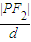 =e=
=e= ,|PF1|=2d,且|PF1|+|PF2|=2a,
,|PF1|=2d,且|PF1|+|PF2|=2a,则|PF1|=2a-|PF2|=2a-
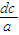 =2d,即d=
=2d,即d=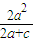 ,
,而|PF1|∈(a-c,a+c),即2d=
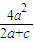 ,
,所以得到
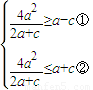 ,由①得:
,由①得: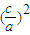 +
+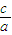 +2≥0,
+2≥0,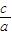 为任意实数;
为任意实数;由②得:
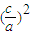 +3
+3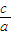 -2≥0,解得
-2≥0,解得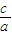 ≥
≥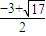 或
或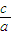 ≤
≤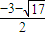 (舍去),
(舍去),所以不等式的解集为:
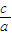 ≥
≥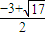 ,即离心率e≥
,即离心率e≥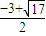 ,又e<1,
,又e<1,所以椭圆离心率的取值范围是[
 ,1).
,1).故答案为:[
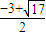 ,1)
,1)点评:此题考查学生掌握椭圆的定义及椭圆简单性质的运用,是一道中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
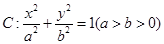 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点,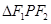 的重心为G,内心I,且有
的重心为G,内心I,且有 (其中
(其中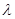 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )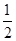 B.
B.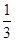 C.
C.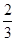 D.
D.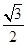
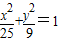 ,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )
,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )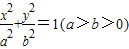 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .