题目内容
已知椭圆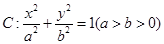 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点,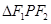 的重心为G,内心I,且有
的重心为G,内心I,且有 (其中
(其中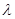 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )
A.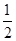 B.
B.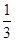 C.
C.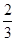 D.
D.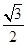
【答案】
A
【解析】
试题分析:设P(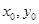 ),∵G为
),∵G为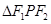 的重心,∴G点坐标为 G(
的重心,∴G点坐标为 G(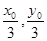 ),∵
),∵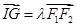 ,∴IG∥x轴,∴I的纵坐标为
,∴IG∥x轴,∴I的纵坐标为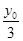 ,在焦点
,在焦点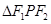 中,
中,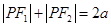 ,
,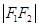 =2c,∴
=2c,∴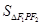 =
=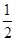 ?
?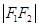 ?
?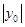 ,又∵I为
,又∵I为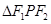 的内心,∴I的纵坐标
的内心,∴I的纵坐标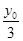 即为内切圆半径,内心I把
即为内切圆半径,内心I把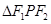 分为三个底分别为
分为三个底分别为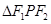 的三边,高为内切圆半径的小三角形,∴
的三边,高为内切圆半径的小三角形,∴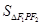 =
=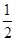 (
(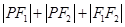 )
)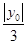 ,∴
,∴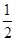 ?
?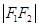 ?
?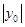 =
=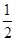 (
(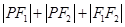 )
)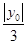 即
即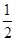 ?2c?
?2c?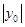 =
=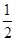 (
(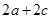 )
)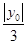 ,∴2c=a,∴椭圆C的离心率e=
,∴2c=a,∴椭圆C的离心率e=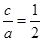 ,故选A
,故选A
考点:本题考查了离心率的求法
点评:求解椭圆中的离心率时往往用到椭圆的概念,此类问题还用到重心坐标公式,三角形内心的意义及其应用

练习册系列答案
相关题目
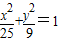 ,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )
,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )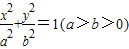 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .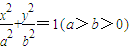 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .