题目内容
已知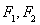 是椭圆E:
是椭圆E: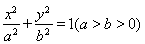 的两个焦点,抛物线
的两个焦点,抛物线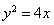 的焦点为椭圆E的一个焦点,直线y=
的焦点为椭圆E的一个焦点,直线y=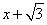 上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
上到焦点F1,F2距离之和最小的点P恰好在椭圆E上,
(Ⅰ)求椭圆E的方程;
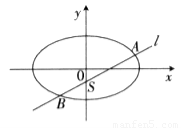
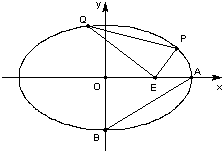
(Ⅱ)如图,过点 的动直线
的动直线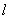 交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。
交椭圆于A、B两点,是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出点M的坐标;若不存在,请说明理由。
【答案】
(Ⅰ)椭圆方程为 ;(Ⅱ)存在定点M
;(Ⅱ)存在定点M ,使以
,使以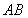 为直径的圆恒过这个定点.
为直径的圆恒过这个定点.
【解析】
试题分析:(Ⅰ)求椭圆E的方程,可用待定系数法求方程,因为抛物线 的焦点为
的焦点为 ,故可得椭圆E:的两个焦点
,故可得椭圆E:的两个焦点 ,即
,即 ,由题意直线y=
,由题意直线y= 上到焦点F1,F2距离之和最小,可用对称法求最小值,即求出点
上到焦点F1,F2距离之和最小,可用对称法求最小值,即求出点 关于直线
关于直线 的对称点为
的对称点为 最小值为
最小值为 ,此时的点P恰好在椭圆E上,故
,此时的点P恰好在椭圆E上,故 ,可得
,可得 ,从而得
,从而得 ,这样就得椭圆E的方程;(Ⅱ)这是探索性命题,可假设存在定点M,使以AB为直径的圆恒过这个点,此时当AB
,这样就得椭圆E的方程;(Ⅱ)这是探索性命题,可假设存在定点M,使以AB为直径的圆恒过这个点,此时当AB 轴时,以AB为直径的圆的方程为:
轴时,以AB为直径的圆的方程为: ,当AB
,当AB 轴时,以AB为直径的圆的方程为:
轴时,以AB为直径的圆的方程为: ,解得两圆公共点
,解得两圆公共点 .因此所求的点
.因此所求的点 如果存在,只能是
如果存在,只能是 .由此能够导出以AB为直径的圆恒过定点M
.由此能够导出以AB为直径的圆恒过定点M .
.
试题解析:(Ⅰ)由抛物线的焦点可得: ,
,
点 关于直线
关于直线 的对称点为
的对称点为
故 ,
,
因此 ,椭圆方程为
,椭圆方程为 。(4分)
。(4分)
(Ⅱ)假设存在定点M,使以AB为直径的圆恒过这个点。
当AB 轴时,以AB为直径的圆的方程为:
轴时,以AB为直径的圆的方程为: …………… ①
…………… ①
当AB 轴时,以AB为直径的圆的方程为:
轴时,以AB为直径的圆的方程为: …………②
…………②
由①②知定点M 。(6分)
。(6分)
下证:以AB为直径的圆恒过定点M 。
。
设直线 ,代入
,代入 ,有
,有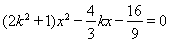 。
。
设 ,则
,则 。
。
则 ,
,


 在
在 轴上存在定点M
轴上存在定点M ,使以
,使以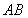 为直径的圆恒过这个定点。(14分)
为直径的圆恒过这个定点。(14分)
考点:直线与圆锥曲线的综合问题;圆锥曲线的共同特征.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
 已知中心在原点O,焦点在x轴上的椭圆C的离心率为
已知中心在原点O,焦点在x轴上的椭圆C的离心率为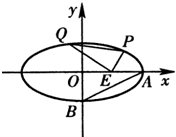 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为