题目内容
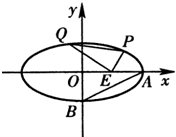 如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
| ||
| 2 |
6
| ||
| 5 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足EP⊥EQ,求
| EP |
| QP |
分析:(Ⅰ)先利用离心率为
得到关于a,b,c之间的关系,再结合点O到直线AB的距离为
,即可求出a,b,c,进而得到椭圆C的标准方程;
(Ⅱ)先利用EP⊥EQ把所求问题转化为
2,再利用点P在抛物线上,利用抛物线上的点的范围限制即可求出
•
的取值范围.
| ||
| 2 |
6
| ||
| 5 |
(Ⅱ)先利用EP⊥EQ把所求问题转化为
| EP |
| EP |
| QP |
解答:解:(Ⅰ)由离心率 e=
=
,得
=
=
∴a=2b①
∵原点O到直线AB的距离为
∴
=
②,
将①代入②,得b2=9,∴a2=36
则椭圆C的标准方程为
+
=1
(Ⅱ)因为EP⊥EQ∴
•
=0
∴
•
=
•(
-
)=
2
设P(x,y),则
+
=1,即 y2=9-
∴
•
=
2=(x-3)2+y2=x2-6x+9+9-
=
(x-4)2+6
∵-6≤x≤6,∴6≤
(x-4)2+6≤81
则
•
的最小值为:6.
| c |
| a |
| ||
| 2 |
| b |
| a |
| 1-e2 |
| 1 |
| 2 |
∵原点O到直线AB的距离为
6
| ||
| 5 |
∴
| ab | ||
|
6
| ||
| 5 |
将①代入②,得b2=9,∴a2=36
则椭圆C的标准方程为
| x2 |
| 36 |
| y2 |
| 9 |
(Ⅱ)因为EP⊥EQ∴
| EP |
| EQ |
∴
| EP |
| QP |
| EP |
| EP |
| EQ |
| EP |
设P(x,y),则
| x2 |
| 36 |
| y2 |
| 9 |
| x2 |
| 4 |
∴
| EP |
| QP |
| EP |
| x2 |
| 4 |
| 3 |
| 4 |
∵-6≤x≤6,∴6≤
| 3 |
| 4 |
则
| EP |
| QP |
点评:本题主要考查直线与圆锥曲线的综合问题.解决第一问的关键是利用条件列出关于a,b,c之间的方程.第二问重点是数量积的应用,二次函数的最值的应用,考查计算能力,转化思想.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
 如图,已知中心在原点且焦点在x轴上的椭圆E经过点A(3,1),离心率
如图,已知中心在原点且焦点在x轴上的椭圆E经过点A(3,1),离心率 如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为
如图,已知中心在原点0、焦点在x轴上的椭圆T过点M(2,1),离心率为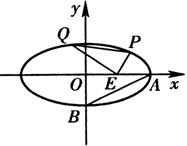
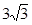 ,
,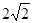 ),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.
),且它的左焦点F1将长轴分成2∶1,F2是椭圆的右焦点.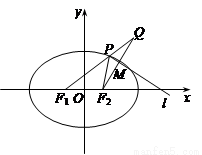 (1)求椭圆的标准方程;
(1)求椭圆的标准方程;