题目内容
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.(I)设点P分有向线段
 所成的比为λ,证明:
所成的比为λ,证明:
(Ⅱ)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.
【答案】分析:(Ⅰ)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程x2=4y得x2-4kx-4m=0.设A、B两点的坐标分别是(x1,y1)、(x2,y2),x1x2=-4m.由点P(0,m)分有向线段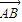 所成的比为λ,得
所成的比为λ,得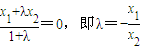 .由此可以推出
.由此可以推出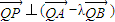 .
.
(Ⅱ)由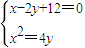 得点A、B的坐标分别是(6,9)、(-4,4).设圆C的方程是(x-a)2+(y-b)2=r2,则
得点A、B的坐标分别是(6,9)、(-4,4).设圆C的方程是(x-a)2+(y-b)2=r2,则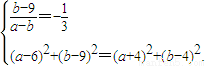 解得
解得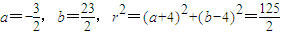 .所以圆C的方程是x2+y2+3x-23y+72=0.
.所以圆C的方程是x2+y2+3x-23y+72=0.
解答:解:(Ⅰ)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程x2=4y得x2-4kx-4m=0.①
设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根.
所以x1x2=-4m.
由点P(0,m)分有向线段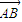 所成的比为λ,
所成的比为λ,
得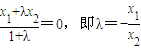 .
.
又点Q是点P关于原点的对称点,
故点Q的坐标是(0,-m),从而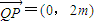 .
.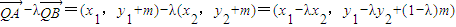 .
.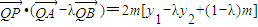 =
=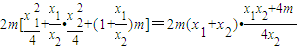 =
=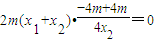 .
.
所以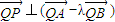 .
.
(Ⅱ)由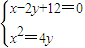 得点A、B的坐标分别是(6,9)、(-4,4).
得点A、B的坐标分别是(6,9)、(-4,4).
由x2=y得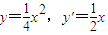 ,
,
所以抛物线x2=4y在点A处切线的斜率为y'|x=6=3
设圆C的方程是(x-a)2+(y-b)2=r2,
则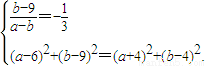
解之得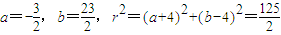 .
.
所以圆C的方程是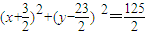 ,
,
即x2+y2+3x-23y+72=0.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细求解.
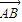 所成的比为λ,得
所成的比为λ,得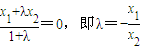 .由此可以推出
.由此可以推出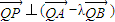 .
.(Ⅱ)由
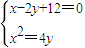 得点A、B的坐标分别是(6,9)、(-4,4).设圆C的方程是(x-a)2+(y-b)2=r2,则
得点A、B的坐标分别是(6,9)、(-4,4).设圆C的方程是(x-a)2+(y-b)2=r2,则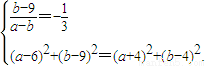 解得
解得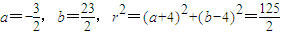 .所以圆C的方程是x2+y2+3x-23y+72=0.
.所以圆C的方程是x2+y2+3x-23y+72=0.解答:解:(Ⅰ)依题意,可设直线AB的方程为y=kx+m,代入抛物线方程x2=4y得x2-4kx-4m=0.①
设A、B两点的坐标分别是(x1,y1)、(x2,y2),则x1、x2是方程①的两根.
所以x1x2=-4m.
由点P(0,m)分有向线段
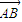 所成的比为λ,
所成的比为λ,得
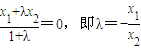 .
.又点Q是点P关于原点的对称点,
故点Q的坐标是(0,-m),从而
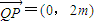 .
.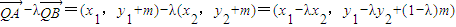 .
.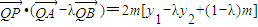 =
=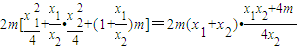 =
=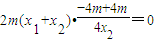 .
.所以
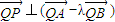 .
.(Ⅱ)由
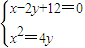 得点A、B的坐标分别是(6,9)、(-4,4).
得点A、B的坐标分别是(6,9)、(-4,4).由x2=y得
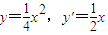 ,
,所以抛物线x2=4y在点A处切线的斜率为y'|x=6=3
设圆C的方程是(x-a)2+(y-b)2=r2,
则
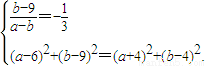
解之得
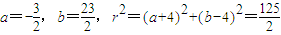 .
.所以圆C的方程是
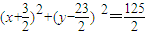 ,
,即x2+y2+3x-23y+72=0.
点评:本题考查直线和圆锥曲线的位置关系,解题时要认真审题,仔细求解.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A,B两点,点Q是点P关于原点的对称点. 如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线交于A(x1,y1),B(x2,y2)两点.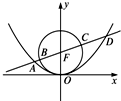 如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则
如图,过抛物线x2=4y焦点的直线依次交抛物线与圆x2+(y-1)2=1于点A、B、C、D,则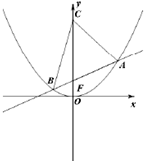 (2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).
(2012•绍兴模拟)如图,过抛物线x2=4y焦点F的直线l与抛物线交于A,B两点(A在第一象限),点C(0,t)(t>1).