题目内容
7.己知函数f(x)=(a+1)lnx+x-$\frac{a}{x}$,其中a∈R.(I)求f(x)的单调区间;
(Ⅱ)若在[1,e]上存在x0,使得f(x0)<0成立,求a的取值范围.
分析 (Ⅰ)先求出函数的单调区间,通过讨论a的范围,确定函数的单调性;(Ⅱ)通过讨论a的范围,得到f(x)在[1,e]的单调性,求出[1,e]的最小值即可求出a的范围.
解答 解:(Ⅰ)函数f(x)的定义域是(0,+∞),
f′(x)=$\frac{a+1}{x}$+1+$\frac{a}{{x}^{2}}$=$\frac{(x+1)(x+a)}{{x}^{2}}$,
①a≥0时,f′(x)>0在(0,+∞)恒成立,
∴f(x)在(0,+∞)递增;
②a<0时,令f′(x)>0,解得:x>-a,令f′(x)<0,解得:x<-a,
∴f(x)在(0,-a)递减,在(-a,+∞)递增;
(Ⅱ)①由(Ⅰ)得:-a≤1即a≥-1时:f(x)在[1,e]递增,
若在[1,e]上存在x0,使得f(x0)<0成立,
只需f(1)=1-a<0即可,解得:a>1;
②若1<-a<e即-e<a<-1时:
f(x)在[1,-a)递减,在(-a,e]递增,
若在[1,e]上存在x0,使得f(x0)<0成立,
只需f(-a)<0即可,
即(a+1)ln(-a)+(-a)+1<0,
即ln(-a)>1-$\frac{2}{a+1}$,
而1<-a<e,则0<ln(-a)<1,1-$\frac{2}{a+1}$>1,
∴ln(-a)>1-$\frac{2}{a+1}$,无解;
③若-a≥e,即a≤-e时:f(x)在[1,e]递减,
若在[1,e]上存在x0,使得f(x0)<0成立,
只需f(e)<0即可,
即(a+1)+e-$\frac{a}{e}$<0,解得:a<-$\frac{e(e+1)}{e-1}$;
综上:a>1或a<-$\frac{e(e+1)}{e-1}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,分类讨论思想,是一道中档题.

| A. | (n-1)2n+1-2 | B. | (n-1)2n+1+2 | C. | (n+1)2n+1-2 | D. | (n+1)2n+1+2 |
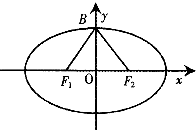 设F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,B为短轴的一个端点,且△F1BF2是边长为2的等边三角形.
设F1,F2分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点,B为短轴的一个端点,且△F1BF2是边长为2的等边三角形.