题目内容
12.定义$\sum_{i=1}^{n}$ai=a1+a2+…+an,并设f(x)=$\frac{{a}^{x}}{{a}^{x}+\sqrt{a}}$,求$\sum _{j=1}^{2003}$f($\frac{i}{2004}$).分析 计算f(x)+f(1-x)=1,设S=$\sum_{j=1}^{2003}$f($\frac{j}{2004}$),运用倒序相加求和,即可得到所求值.
解答 解:f(x)=$\frac{{a}^{x}}{{a}^{x}+\sqrt{a}}$,
f(1-x)=$\frac{{a}^{1-x}}{{a}^{1-x}+\sqrt{a}}$=$\frac{a}{a+{a}^{x}\sqrt{a}}$=$\frac{\sqrt{a}}{\sqrt{a}+{a}^{x}}$,
即有f(x)+f(1-x)=$\frac{{a}^{x}}{{a}^{x}+\sqrt{a}}$+$\frac{\sqrt{a}}{\sqrt{a}+{a}^{x}}$=1,
可设S=$\sum_{j=1}^{2003}$f($\frac{j}{2004}$)=f($\frac{1}{2004}$)+f($\frac{2}{2004}$)+…+f($\frac{2003}{2004}$),
又S=f($\frac{2003}{2004}$)+f($\frac{2002}{2004}$)+…+f($\frac{2}{2004}$)+f($\frac{1}{2004}$),
则2S=[f($\frac{1}{2004}$)+f($\frac{2003}{2004}$)]+[f($\frac{2}{2004}$)+f($\frac{2002}{2004}$)]+…+[f($\frac{2003}{2004}$)+f($\frac{1}{2004}$)]
=1+1+…+1=2003,
则S=$\frac{2003}{2}$.
即有$\sum_{j=1}^{2003}$f($\frac{j}{2004}$)=$\frac{2003}{2}$.
点评 本题考查函数的性质和运用,考查倒序相加求和的运用,考查运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案( )
| A. | 10 | B. | -10 | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
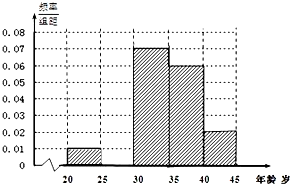 2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿,某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组:[20,25),[25,30),[30,35),[35,40),[40,45),根据调查结果得出年龄情况残缺的频率分布直方图如图所示.
2015年7月16日,电影《捉妖记》上映,上映至今全国累计票房已超过20亿,某影院为了解观看此部电影的观众年龄的情况,在某场次的100名观众中随机调查了20名观众,已知抽到的观众年龄可分成5组:[20,25),[25,30),[30,35),[35,40),[40,45),根据调查结果得出年龄情况残缺的频率分布直方图如图所示.