题目内容
如图,抛物线C1:y2=8x与双曲线 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.(Ⅰ)求双曲线C2的方程;
(Ⅱ)以F1为圆心的圆M与双曲线的一条渐近线相切,圆N:(x-2)2+y2=1.平面上有点P满足:存在过点P的无穷多对互相垂直的直线l1,l2,它们分别与圆M,N相交,且直线l1被圆M截得的弦长与直线l2被圆N截得的弦长的比为
 ,试求所有满足条件的点P的坐标.
,试求所有满足条件的点P的坐标.
【答案】分析:(Ⅰ)由题意知双曲线C2的焦点为F1(-2,0)、F2(2,0),设A(x,y)在抛物线C1:y2=8x上,且|AF2|=5,由抛物线的定义得,x+2=5,x=3,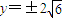 ,
,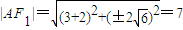 ,由此可知双曲线的方程.
,由此可知双曲线的方程.
(Ⅱ)设圆M的方程为:(x+2)2+y2=r2,双曲线的渐近线方程为: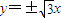 ,故圆M:(x+2)2+y2=3.由此入手可推导出所有满足条件的点P的坐标.
,故圆M:(x+2)2+y2=3.由此入手可推导出所有满足条件的点P的坐标.
解答:解:(Ⅰ)∵抛物线C1:y2=8x的焦点为F2(2,0),
∴双曲线C2的焦点为F1(-2,0)、F2(2,0),(1分)
设A(x,y)在抛物线C1:y2=8x上,且|AF2|=5,
由抛物线的定义得,x+2=5,∴x=3,(2分)
∴y2=8×3,∴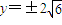 ,(3分)
,(3分)
∴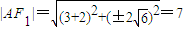 ,(4分)
,(4分)
又∵点A在双曲线上,
由双曲线定义得,2a=|7-5|=2,∴a=1,(5分)
∴双曲线的方程为: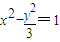 .(6分)
.(6分)
(Ⅱ)设圆M的方程为:(x+2)2+y2=r2,
双曲线的渐近线方程为: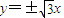 ,
,
∵圆M与渐近线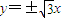 相切,∴
相切,∴
圆M的半径为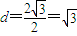 ,(7分)
,(7分)
故圆M:(x+2)2+y2=3,(8分)
设点P(x,y),则l1的方程为y-y=k(x-x),
即kx-y-kx+y=0,l2的方程为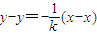 ,
,
即x+ky-x-ky=0,
∴点M到直线l1的距离为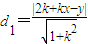 ,
,
点N到直线l2的距离为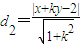 ,
,
∴直线l1被圆M截得的弦长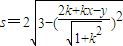 ,
,
直线l2被圆N截得的弦长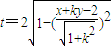 ,(11分)
,(11分)
由题意可得,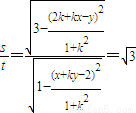 ,
,
即3(x+ky-2)2=(2k+kx-y)2,
∴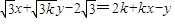 ①
①
或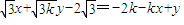 ②(12分)
②(12分)
由①得: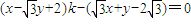 ,
,
∵该方程有无穷多组解,
∴ ,解得
,解得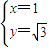 ,
,
点P的坐标为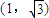 .(13分)
.(13分)
由②得: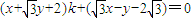 ,
,
∵该方程有无穷多组解,
∴ ,解得
,解得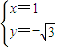 ,
,
点P的坐标为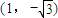 .
.
∴满足条件的点P的坐标为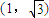 或
或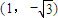 .(14分)
.(14分)
点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细解答,注意公式的灵活运用.
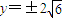 ,
,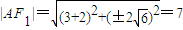 ,由此可知双曲线的方程.
,由此可知双曲线的方程.(Ⅱ)设圆M的方程为:(x+2)2+y2=r2,双曲线的渐近线方程为:
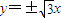 ,故圆M:(x+2)2+y2=3.由此入手可推导出所有满足条件的点P的坐标.
,故圆M:(x+2)2+y2=3.由此入手可推导出所有满足条件的点P的坐标.解答:解:(Ⅰ)∵抛物线C1:y2=8x的焦点为F2(2,0),
∴双曲线C2的焦点为F1(-2,0)、F2(2,0),(1分)
设A(x,y)在抛物线C1:y2=8x上,且|AF2|=5,
由抛物线的定义得,x+2=5,∴x=3,(2分)
∴y2=8×3,∴
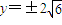 ,(3分)
,(3分)∴
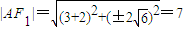 ,(4分)
,(4分)又∵点A在双曲线上,
由双曲线定义得,2a=|7-5|=2,∴a=1,(5分)
∴双曲线的方程为:
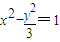 .(6分)
.(6分)(Ⅱ)设圆M的方程为:(x+2)2+y2=r2,
双曲线的渐近线方程为:
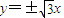 ,
,∵圆M与渐近线
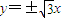 相切,∴
相切,∴圆M的半径为
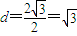 ,(7分)
,(7分)故圆M:(x+2)2+y2=3,(8分)
设点P(x,y),则l1的方程为y-y=k(x-x),
即kx-y-kx+y=0,l2的方程为
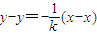 ,
,即x+ky-x-ky=0,
∴点M到直线l1的距离为
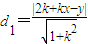 ,
,点N到直线l2的距离为
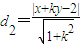 ,
,∴直线l1被圆M截得的弦长
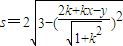 ,
,直线l2被圆N截得的弦长
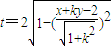 ,(11分)
,(11分)由题意可得,
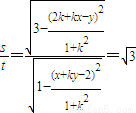 ,
,即3(x+ky-2)2=(2k+kx-y)2,
∴
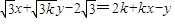 ①
①或
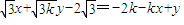 ②(12分)
②(12分)由①得:
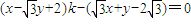 ,
,∵该方程有无穷多组解,
∴
 ,解得
,解得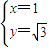 ,
,点P的坐标为
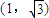 .(13分)
.(13分)由②得:
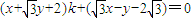 ,
,∵该方程有无穷多组解,
∴
 ,解得
,解得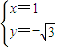 ,
,点P的坐标为
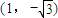 .
.∴满足条件的点P的坐标为
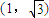 或
或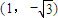 .(14分)
.(14分)点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
相关题目
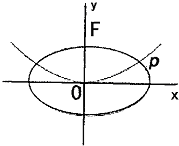 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: (2012•河北模拟)如图,抛物线C1:y2=2px(p>0)的焦点为F,A为C1上的点,以F为圆心,
(2012•河北模拟)如图,抛物线C1:y2=2px(p>0)的焦点为F,A为C1上的点,以F为圆心, 的离心率
的离心率 ,C1与C2在第一象限的交点为
,C1与C2在第一象限的交点为 ,
, 。
。 
 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-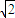 时,切线MA的斜率为-
时,切线MA的斜率为- .
. 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1- 时,切线MA的斜率为-
时,切线MA的斜率为- .
.