题目内容

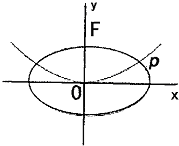精英家教网如图，抛物线C1：x2=2py（p＞0）的焦点为F，椭圆C2：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，C1与C2在第一象限的交点为P（
3
，
1
2
）
（1）求抛物线C1及椭圆C2的方程；
（2）已知直线l：y=kx+t（k≠0，t＞0）与椭圆C2交于不同两点A、B，点M满足
AM
+
BM
=
0
，直线FM的斜率为k1，试证明k•k1＞
-1
4
．
分析：（1）借助于抛物线过点P，先求抛物线方程，再利用离心率e=
3
2
，求椭圆方程；
（2）点M满足
AM
+
BM
=
0
，等价于点M为线段AB的中点，从而表达出斜率，再进行证明．
解答：解：（1）将P（
3
，
1
2
）代入x2=2py得p=3，∴抛物线C1的方程为x2=6y，焦点F（0，
3
2
）
把P（
3
，
1
2
）代入
x2
a2
+
y2
b2
=1得
3
a2
+
1
4b2
=1，又e=
3
2
，∴a=2，b=1故椭圆C2的方程为
x2
4
+
y2
1
=1
（2）由直线l：y=kx+t与
x2
4
+
y2
1
=1联立得（1+4k2）x2+8ktx+4（t2-1）=0，△＞0得1+4k2＞t2
设A（x1，y1），B（x2，y2）则x1+x2=
-8kt
1+4k2

由题意点M为线段AB的中点，设M（xM，yM），
∴xM=
-4kt
1+4k2
，yM=
t
1+4k2
，
∴k1=
2t-3(1+4k2)
-8kt
∴kk1＞
3t2-2t
8t
=
3t -2
8
＞-
1
4
点评：本题主要考查圆锥曲线相交，求圆锥曲线问题，利用了待定系数法，同时考查了直线与曲线相交问题，利用设而不求法进行证明．
练习册系列答案
相关题目
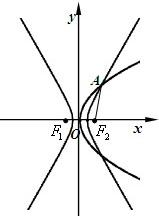精英家教网如图，抛物线C1：y2=8x与双曲线C2：
x2
a2
-
y2
b2
=1(a＞0，b＞0)有公共焦点F2，点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（Ⅰ）求双曲线C2的方程；
（Ⅱ）以F1为圆心的圆M与双曲线的一条渐近线相切，圆N：（x-2）2+y2=1．平面上有点P满足：存在过点P的无穷多对互相垂直的直线l1，l2，它们分别与圆M，N相交，且直线l1被圆M截得的弦长与直线l2被圆N截得的弦长的比为
3
：1，试求所有满足条件的点P的坐标．
如图，抛物线C1：y2=8x与双曲线C2：
x2
a2
-
y2
b2
=1（a＞0，b＞0）有公共焦点F2，点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（1）求双曲线C2的方程；
（2）以F1为圆心的圆M与双曲线的一条渐近线相切，圆N：（x-2）2+y2=1，已知点P（1，
3
），过点P作互相垂直且分别与圆M圆N相交的直线l1，l2，设l1被圆M截得的弦长为s，l2被圆N截得的弦长为t，
s
t
是否为定值？请说明理由．
如图过抛物线C1：x2=4y的对称轴上一点P（0，m）（m＞0）作直线l与抛物线交于A（x1，y1），B（x2，y2）两点，点Q是P关于原点的对称点，以P，Q为焦点的椭圆为C2．
（1）求证：x1x2为定值；
（2）若l的方程为x-2y+4=0，且C1，C2以及直线l有公共点，求C2的方程；
（3）设
AP
=λ
PB
，若
QP
⊥(
QA
-μ
QB
)，求证：λ=μ
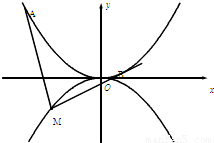如图，抛物线C1：x2=4y，C2：x2=-2py（p＞0），点M（x，y）在抛物线C2上，过M作C1的切线，切点为A，B（M为原点O时，A，B重合于O），当x=1-时，切线MA的斜率为-．
（I）求P的值；
（II）当M在C2上运动时，求线段AB中点N的轨迹方程（A，B重合于O时，中点为O）．
如图，抛物线C1：y2=8x与双曲线有公共焦点F2，点A是曲线C1，C2在第一象限的交点，且|AF2|=5．
（1）求双曲线C2的方程；
（2）以F1为圆心的圆M与双曲线的一条渐近线相切，圆N：（x-2）2+y2=1．已知点，过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2，设l1被圆M截得的弦长为s，l2被圆N截得的弦长为t．是否为定值？请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网