题目内容
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2: 的离心率
的离心率 ,C1与C2在第一象限的交点为
,C1与C2在第一象限的交点为 ,
,
(Ⅰ)求抛物线C1及椭圆C2的方程;
(Ⅱ)已知直线l:y=kx+t(k≠0,t>0)与椭圆C2交于不同两点A,B,点M满足 ,直线FM的斜率为k1,试证明
,直线FM的斜率为k1,试证明 。
。
 的离心率
的离心率 ,C1与C2在第一象限的交点为
,C1与C2在第一象限的交点为 ,
,(Ⅰ)求抛物线C1及椭圆C2的方程;
(Ⅱ)已知直线l:y=kx+t(k≠0,t>0)与椭圆C2交于不同两点A,B,点M满足
 ,直线FM的斜率为k1,试证明
,直线FM的斜率为k1,试证明 。
。 
解:(Ⅰ)将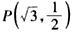 代入x2=2py,得p=3,
代入x2=2py,得p=3,
∴抛物线C1的方程为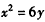 ,焦点
,焦点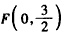 ,
,
把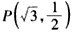 代入
代入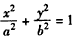 ,得
,得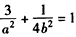 ,
,
又∵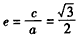 ,
,
∴ ,
,
解得:a=2,b=1,
故椭圆C2的方程为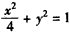 。
。
(Ⅱ)由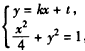 ,得
,得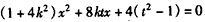 ,
,
令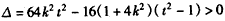 ,
,
得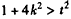 , ①
, ①
设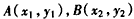 ,
,
∴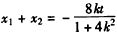 ,
,
∵ ,
,
∴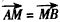 ,即点M为线段AB的中点,
,即点M为线段AB的中点,
设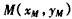 ,
,
∴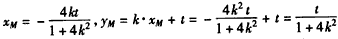 ,
,
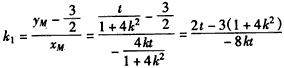 ,
,
∴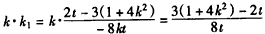 ,
,
∵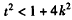 ,
,
∴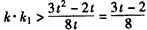 ,
,
又∵t>0,
∴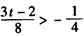 ,即
,即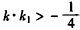 。
。
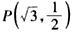 代入x2=2py,得p=3,
代入x2=2py,得p=3,∴抛物线C1的方程为
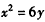 ,焦点
,焦点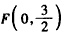 ,
,把
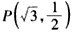 代入
代入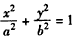 ,得
,得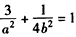 ,
,又∵
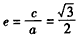 ,
,∴
 ,
,解得:a=2,b=1,
故椭圆C2的方程为
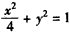 。
。(Ⅱ)由
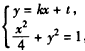 ,得
,得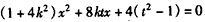 ,
,令
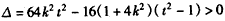 ,
,得
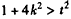 , ①
, ①设
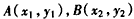 ,
,∴
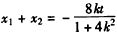 ,
,∵
 ,
,∴
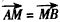 ,即点M为线段AB的中点,
,即点M为线段AB的中点,设
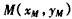 ,
,∴
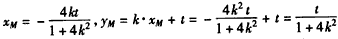 ,
,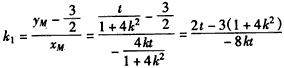 ,
,∴
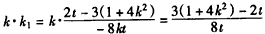 ,
,∵
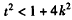 ,
,∴
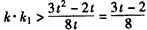 ,
,又∵t>0,
∴
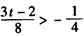 ,即
,即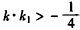 。
。
练习册系列答案
相关题目
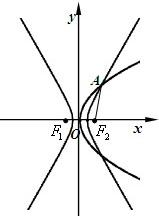 如图,抛物线C1:y2=8x与双曲线
如图,抛物线C1:y2=8x与双曲线 如图过抛物线
如图过抛物线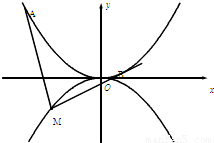 如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1-
如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x,y)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x=1- 时,切线MA的斜率为-
时,切线MA的斜率为- .
. 有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5.
有公共焦点F2,点A是曲线C1,C2在第一象限的交点,且|AF2|=5. ,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t.
,过点P作互相垂直且分别与圆M、圆N相交的直线l1和l2,设l1被圆M截得的弦长为s,l2被圆N截得的弦长为t. 是否为定值?请说明理由.
是否为定值?请说明理由.