题目内容
抛物线y=x2+x+2上点(1,4)处的切线的斜率是________,该切线方程为________________.
3,3x-y+1=0
【解析】Δy=(1+d)2+(1+d)+2-(12+1+2)=3d+d2,故y′|x=1=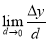 =
=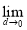 (3+d)=3.∴切线的方程为y-4=3(x-1),即3x-y+1=0.
(3+d)=3.∴切线的方程为y-4=3(x-1),即3x-y+1=0.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
题目内容
抛物线y=x2+x+2上点(1,4)处的切线的斜率是________,该切线方程为________________.
3,3x-y+1=0
【解析】Δy=(1+d)2+(1+d)+2-(12+1+2)=3d+d2,故y′|x=1=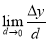 =
=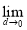 (3+d)=3.∴切线的方程为y-4=3(x-1),即3x-y+1=0.
(3+d)=3.∴切线的方程为y-4=3(x-1),即3x-y+1=0.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案