题目内容
已知cos2α=
,有α为第三象限角,则tan2α= .
| 9 |
| 25 |
考点:二倍角的正切
专题:三角函数的求值
分析:依题意,利用同角三角函数间的关系式可求得tanα=
,再利用二倍角的正切即可求得答案.
| 4 |
| 3 |
解答:
解:∵cos2α=
,有α为第三象限角,
∴cosα=-
,sinα=-
=-
,
∴tanα=
,
∴tan2α=
=
=-
.
故答案为:-
.
| 9 |
| 25 |
∴cosα=-
| 3 |
| 5 |
| 1-cos2α |
| 4 |
| 5 |
∴tanα=
| 4 |
| 3 |
∴tan2α=
| 2tanα |
| 1-tan2α |
| ||
1-
|
| 24 |
| 7 |
故答案为:-
| 24 |
| 7 |
点评:本题考查同角三角函数间的关系式与二倍角的正切公式的应用,考查运算求解能力,属于中档题.

练习册系列答案
相关题目
函数y=
+
的值域为( )
| x-2 |
| 9-3x |
A、[1,
| ||
B、[
| ||
| C、[1,2] | ||
| D、[2,3] |
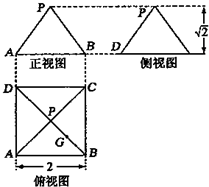 某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.