Question

【题目】已知全集U={x|x≤4}，集合A={x|﹣2＜x＜3}，B={x|﹣3≤x≤2}，求A∩B，（UA）∪B，A∩（UB）．

Answer 1

【答案】解：如图所示，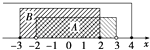

∵A={x|﹣2＜x＜3}，B={x|﹣3≤x≤2}，
∴UA={x|x≤﹣2，或3≤x≤4}，UB={x|x＜﹣3，或2＜x≤4}．
故A∩B={x|﹣2＜x≤2}，（UA）∪B={x|x≤2，或3≤x≤4}，A∩（UB）={x|2＜x＜3}
【解析】全集U={x|x≤4}，集合A={x|﹣2＜x＜3}，B={x|﹣3≤x≤2}，求出CUA，CUB，由此能求出A∩B，（UA）∪B，A∩（UB）．画数轴是最直观的方法．
【考点精析】掌握交、并、补集的混合运算是解答本题的根本，需要知道求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合Venn图或数轴进而用集合语言表达，增强数形结合的思想方法．