题目内容
已知直线x=k与y=log5x及y=log5（x+4）的图象相交，且两交点之间的距离为
．若k=a+
，这里a、b均为整数，则a+b的值为（ ）
| 1 |
| 2 |
| b |
分析：由题设知
=log5(a+
+4) -log5(a+
)=log5 (1+
)，即
=
-1，所以(
-1)(a+
)=4，由a、b均为整数，知b=5，a=1，a+b=6．
| 1 |
| 2 |
| b |
| b |
| 4 | ||
a+
|
| 4 | ||
a+
|
| 5 |
| 5 |
| b |
解答：解：∵直线x=k与y=log5x及y=log5（x+4）的图象相交，
且两交点之间的距离为
．k=a+
，
∴
=log5(a+
+4) -log5(a+
)=log5 (1+
)，
∴
=
-1，
∴(
-1)(a+
)=4，
∵a、b均为整数，
∴b=5，a=1，a+b=6．
故选A．
且两交点之间的距离为
| 1 |
| 2 |
| b |
∴
| 1 |
| 2 |
| b |
| b |
| 4 | ||
a+
|
∴
| 4 | ||
a+
|
| 5 |
∴(
| 5 |
| b |
∵a、b均为整数，
∴b=5，a=1，a+b=6．
故选A．
点评：本题考查对数函数的图象和性质，解题时要认真审题，注意对数函数的性质的灵活运用．
练习册系列答案
相关题目
．若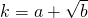
，这里a、b均为整数，则a+b的值为