题目内容
已知a∈R,函数f(x)=x|x-a|.
(Ⅰ)当a=2时,作出图形并写出函数y=f(x)的单调递增区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间(-
-1,2]的值域;
(Ⅲ)设a≠0,函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围(用a表示).
(Ⅰ)当a=2时,作出图形并写出函数y=f(x)的单调递增区间;
(Ⅱ)当a=-2时,求函数y=f(x)在区间(-
| 2 |
(Ⅲ)设a≠0,函数f(x)在(m,n)上既有最大值又有最小值,请分别求出m、n的取值范围(用a表示).
分析:(Ⅰ)当a=2时,f(x)=x|x-2|=
,作出图象即可写出函数y=f(x)的单调递增区间;
(Ⅱ)当a=-2时,f(x)=x|x+2|=
,可求得函数y=f(x)在区间(-
-1,2]的值域为[-1,8];
(Ⅲ)设a≠0,f(x)=x|x-a|=
,函数f(x)在(m,n)上既有最大值又有最小值,须m<
,n>a.
|
(Ⅱ)当a=-2时,f(x)=x|x+2|=
|
| 2 |
(Ⅲ)设a≠0,f(x)=x|x-a|=
|
| a |
| 2 |
解答:解:(Ⅰ)当a=2时,f(x)=x|x-2|=
,作出图象,
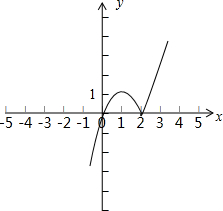
由图可知,函数y=f(x)的单调递增区间为(-∞,1],[2,+∞);
(Ⅱ)当a=-2时,f(x)=x|x+2|=
,
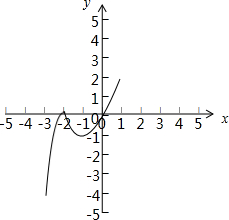
∵f(-1-
)=-(-1-
)2-2(-1-
)=-1,f(-1)=(-1)2+2×(-1)=-1,f(2)=4+4=8,
∴函数y=f(x)在区间(-
-1,2]的值域为[-1,8];
(Ⅲ)∵a≠0,f(x)=x|x-a|=
,函数f(x)有两个零点:0和a,
若a>0,在(-∞,
)上单调递增,在(
,a)上单调递减,在(a,+∞)上单调递增.
为使在区间(m,n)上既有最大值又有最小值,必须0≤m<
,n≤
a.
若a<0,在(-∞,a)上单调递增,在(a,
)上单调递减,在(
,+∞)上单调递增.
为使在区间(m,n)上既有最大值又有最小值,必须m≥
a,n≤0.
|
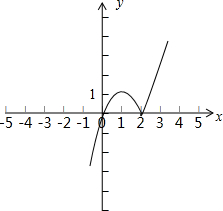
由图可知,函数y=f(x)的单调递增区间为(-∞,1],[2,+∞);
(Ⅱ)当a=-2时,f(x)=x|x+2|=
|
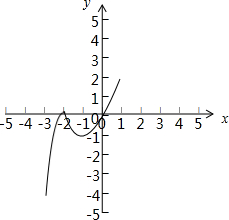
∵f(-1-
| 2 |
| 2 |
| 2 |
∴函数y=f(x)在区间(-
| 2 |
(Ⅲ)∵a≠0,f(x)=x|x-a|=
|
若a>0,在(-∞,
| a |
| 2 |
| a |
| 2 |
为使在区间(m,n)上既有最大值又有最小值,必须0≤m<
| a |
| 2 |
1+
| ||
| 2 |
若a<0,在(-∞,a)上单调递增,在(a,
| a |
| 2 |
| a |
| 2 |
为使在区间(m,n)上既有最大值又有最小值,必须m≥
1+
| ||
| 2 |
点评:本题考查带绝对值的函数,着重考查分段函数的图象与性质,考查函数的单调性,最值,考查化归思想,数形结合思想,分类讨论思想的综合运用,属于难题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目