题目内容
已知a∈R,函数f(x)=| 1 |
| 12 |
| a+1 |
| 2 |
(Ⅰ)如果函数g(x)=f′(x)是偶函数,求f(x)的极大值和极小值;
(Ⅱ)如果函数f(x)是(-∞,?+∞)上的单调函数,求a的取值范围.
分析:(Ⅰ)据次数为奇数的系数为0,时函数为偶函数求出a;求出导函数的根,判断根左右两边导函数的正负号,据极值的定义求出极值.
(Ⅱ)f(x)的导函数为二次函数,据函数单调性已知对应的导函数大于等于0恒成立,判别式小于等于0求出a的范围.
(Ⅱ)f(x)的导函数为二次函数,据函数单调性已知对应的导函数大于等于0恒成立,判别式小于等于0求出a的范围.
解答:解:f′(x)=
x2+(a+1)x+(4a+1).
(Ⅰ)∵f'(x)是偶函数,
∴a=-1.
此时f(x)=
x3-3x,f′(x)=
x2-3,
令f'(x)=0,解得:x=±2
.
列表如下: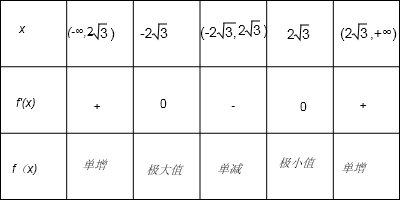
可知:f(x)的极大值为f(-2
)=4
,f(x)的极小值为f(2
)=-4
.
(Ⅱ)∵f′(x)=
x2+(a+1)x+(4a+1),
令△=(a+1)2-4•
•(4a+1)=a2-2a≤0,
解得:0≤a≤2.
这时f'(x)≥0恒成立,
∴函数y=f(x)在(-∞,?+∞)上为单调递增函数.
综上,a的取值范围是{a|0≤a≤2}.
| 1 |
| 4 |
(Ⅰ)∵f'(x)是偶函数,
∴a=-1.
此时f(x)=
| 1 |
| 12 |
| 1 |
| 4 |
令f'(x)=0,解得:x=±2
| 3 |
列表如下:

可知:f(x)的极大值为f(-2
| 3 |
| 3 |
| 3 |
| 3 |
(Ⅱ)∵f′(x)=
| 1 |
| 4 |
令△=(a+1)2-4•
| 1 |
| 4 |
解得:0≤a≤2.
这时f'(x)≥0恒成立,
∴函数y=f(x)在(-∞,?+∞)上为单调递增函数.
综上,a的取值范围是{a|0≤a≤2}.
点评:被天籁村利用导数求函数的极大值、极小值;利用导数解决函数单调性已知求参数范围:函数单增对应导数大于等于0;函数单减对应导数小于等于0恒成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目