题目内容
已知a∈R,函数f(x)=ln(x+1)-x2+ax+2.(1)若函数f(x)在[1,+∞)上为减函数,求实数a的取值范围;
(2)令a=-1,b∈R,已知函数g(x)=b+2bx-x2.若对任意x1∈(-1,+∞),总存在x2∈[-1,+∞),使得f(x1)=g(x2)成立,求实数b的取值范围.
分析:(1)本题知道了函数在(0,1)上是增函数,求a范围,可以转化为f'(x)<0在(1,+∞)上恒成立,由此求解参数范围即可;
(2)分类讨论求出函数g(x)的最小值,使g(x)的最小值恒小于等于f(x)的最小值,从而求出a的取值范围
(2)分类讨论求出函数g(x)的最小值,使g(x)的最小值恒小于等于f(x)的最小值,从而求出a的取值范围
解答:解:(1)函数f(x)在[1,+∞)上为减函数?f′(x)=
-2x+a≤0
在[1,+∞)上恒成立?a≤2x-
在[1,+∞)上恒成立,
令h(x)=2x-
,由h′(x)>0(或利用增函数减减函数)?h(x)在[1,+∞)上为增函数?h(x)min=h(1)=
,
所以a≤
;
(2)若对任意x1∈[-1,+∞),总存在x2∈[-1,+∞),使得f(x1)=g(x2)成立,则函数f(x)在(-1,+∞)上的值域是函数g(x)在[-1,+∞)上的值域的子集.对于函数f(x),因为
a=-1,所以f(x)=ln(x+1)-x2-x+2,定义域(-1,+∞)
f′(x)=
-2x-1=
令f′(x)=0得x1=0x2=-
(舍去).
当x变化时,f(x)与f′(x)的变化情况如下表:
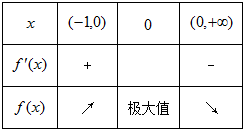
所以f(x)max=f(0)=2?所以f(x)的值域为(-∞,2)
对于函数g(x)=-x2+2bx+b=-(x-b)2+b+b2
①当b≤-1时,g(x)的最大值为g(-1)=-1-b?g(x)值域为(-∞,-1-b]
由-1-b≥2?b≤3;
②当b>-1时,g(x)的最大值为g(b)=b2+b?g(x)值域为(-∞,b2+b]
由b2+b≥2?b≥1或b≤-2(舍去),
综上所述,b的取值范围是(-∞,-3]∪[1.+∞).
| 1 |
| x+1 |
在[1,+∞)上恒成立?a≤2x-
| 1 |
| x+1 |
令h(x)=2x-
| 1 |
| x+1 |
| 3 |
| 2 |
所以a≤
| 3 |
| 2 |
(2)若对任意x1∈[-1,+∞),总存在x2∈[-1,+∞),使得f(x1)=g(x2)成立,则函数f(x)在(-1,+∞)上的值域是函数g(x)在[-1,+∞)上的值域的子集.对于函数f(x),因为
a=-1,所以f(x)=ln(x+1)-x2-x+2,定义域(-1,+∞)
f′(x)=
| 1 |
| x+1 |
| -2x2-3x |
| x+1 |
令f′(x)=0得x1=0x2=-
| 3 |
| 2 |
当x变化时,f(x)与f′(x)的变化情况如下表:

所以f(x)max=f(0)=2?所以f(x)的值域为(-∞,2)
对于函数g(x)=-x2+2bx+b=-(x-b)2+b+b2
①当b≤-1时,g(x)的最大值为g(-1)=-1-b?g(x)值域为(-∞,-1-b]
由-1-b≥2?b≤3;
②当b>-1时,g(x)的最大值为g(b)=b2+b?g(x)值域为(-∞,b2+b]
由b2+b≥2?b≥1或b≤-2(舍去),
综上所述,b的取值范围是(-∞,-3]∪[1.+∞).
点评:本题主要考查了函数的最值及其几何意义,以及分类讨论的思想,解题的关键是对于恒成立的理解,是一道综合题

练习册系列答案
相关题目