题目内容
【题目】已知函数![]() .
.
(1)设![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在其定义域内有两个零点,求实数
在其定义域内有两个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调递增区间为![]() ,无单调递减区间.(2)
,无单调递减区间.(2)![]()
【解析】
(1)对函数f(x)求导,然后构造函数![]() ,通过判断F(x)的单调性和最值即可得到函数f(x)的单调性;(2)“函数
,通过判断F(x)的单调性和最值即可得到函数f(x)的单调性;(2)“函数![]() 在其定义域内有两个零点”可以转化为函数
在其定义域内有两个零点”可以转化为函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同的交点,利用导数的几何意义求解即可得到答案.
上有两个不同的交点,利用导数的几何意义求解即可得到答案.
(1)![]()
函数![]() 的定义域为
的定义域为![]() ,
,
![]()
令![]() ,则
,则![]()
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
所以![]()
所以![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间.
,无单调递减区间.
(2)(法一):![]() 的定义域为
的定义域为![]() ,
,
所以“函数![]() 在其定义域内有两个零点”等价于“方程
在其定义域内有两个零点”等价于“方程![]() 在区间
在区间![]() 内有两个不同的实数根”即方程
内有两个不同的实数根”即方程![]() 在区间
在区间![]() 内有两个不同的实数根
内有两个不同的实数根
故上述问题可以转化为函数![]() 与函数
与函数![]() 的图像在
的图像在![]() 上有两个不同的交点,如图
上有两个不同的交点,如图
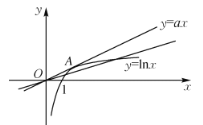
若令过原点且与函数![]() 图像相切的直线斜率为
图像相切的直线斜率为![]() ,由图可得
,由图可得![]()
令切点![]()
由![]() ,得
,得![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() ,解得:
,解得:![]()
于是![]() ,所以
,所以![]()
故实数![]() 的取值范围是
的取值范围是![]()
(法二)![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 在
在![]() 不会有两个零点,不合题意,
不会有两个零点,不合题意,
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
在![]() 上,
上,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
在![]() 上,
上,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
又![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ,
,
要使![]() 有两个零点,则有
有两个零点,则有![]()
即![]()
所以![]()
所以![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】大型综艺节目《最强大脑》中,有一个游戏叫做盲拧魔方,就是玩家先观察魔方状态并进行记忆,记住后蒙住眼睛快速还原魔方,盲拧在外人看来很神奇,其实原理是十分简单的,要学会盲拧也是很容易的.为了解某市盲拧魔方爱好者的水平状况,某兴趣小组在全市范围内随机抽取了![]() 名魔方爱好者进行调查,得到的情况如表所示:
名魔方爱好者进行调查,得到的情况如表所示:
用时(秒) |
|
|
|
|
男性人数 | 15 | 22 | 14 | 9 |
女性人数 | 5 | 11 | 17 | 7 |
附: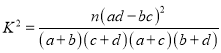 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1)将用时低于![]() 秒的称为“熟练盲拧者”,不低于
秒的称为“熟练盲拧者”,不低于![]() 秒的称为“非熟练盲拧者”.请根据调查数据完成以下
秒的称为“非熟练盲拧者”.请根据调查数据完成以下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为是否为“熟练盲拧者”与性别有关?
的把握认为是否为“熟练盲拧者”与性别有关?
熟练盲拧者 | 非熟练盲拧者 | |
男性 | ||
女性 |
(2)以这![]() 名盲拧魔方爱好者的用时不超过
名盲拧魔方爱好者的用时不超过![]() 秒的频率,代替全市所有盲拧魔方爱好者的用时不超过
秒的频率,代替全市所有盲拧魔方爱好者的用时不超过![]() 秒的概率,每位盲拧魔方爱好者用时是否超过
秒的概率,每位盲拧魔方爱好者用时是否超过![]() 秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取
秒相互独立.那么在该兴趣小组在全市范围内再次随机抽取![]() 名爱好者进行测试,其中用时不超过
名爱好者进行测试,其中用时不超过![]() 秒的人数最有可能(即概率最大)是多少?
秒的人数最有可能(即概率最大)是多少?
【题目】某公司准备上市一款新型轿车零配件,上市之前拟在其一个下属4S店进行连续30天的试销.定价为1000元/件.试销结束后统计得到该4S店这30天内的日销售量(单位:件)的数据如下表:
日销售量 | 40 | 60 | 80 | 100 |
频数 | 9 | 12 | 6 | 3 |
(1)若该4S店试销期间每个零件的进价为650元/件,求试销连续30天中该零件日销售总利润不低于24500元的频率;
(2)试销结束后,这款零件正式上市,每个定价仍为1000元,但生产公司对该款零件不零售,只提供零件的整箱批发,大箱每箱有60件,批发价为550元/件;小箱每箱有45件,批发价为600元/件.该4S店决定每天批发两箱,根据公司规定,当天没销售出的零件按批发价的9折转给该公司的另一下属4S店.假设该4店试销后的连续30天的日销售量(单位:件)的数据如下表:
日销售量 | 50 | 70 | 90 | 110 |
频数 | 5 | 15 | 8 | 2 |
(ⅰ)设该4S店试销结束后连续30天每天批发两大箱,这30天这款零件的总利润;
(ⅱ)以总利润作为决策依据,该4S店试销结束后连续30天每天应该批发两大箱还是两小箱?