Question

（2012•深圳二模）（几何证明选讲选做题）如图，AB是圆O的直径，弦AD和BC相交于点P，连接CD．若∠APB=120°，则

CD

AB

等于

1

2

．

Answer 1

分析：连接AC，BD，先计算CP=

1

2

PA，PD=

1

2

PB，再证明△CPD∽△APB，即可得到结论．

解答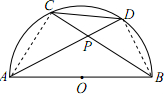：解：连接AC，BD，则∠ACB=∠ADB=90°
∵∠APB=120°，∴∠CPA=∠BPD=60°
∵AB是圆O的直径，
∴∠CAP=∠DBP=30°
∴CP=

1

2

PA，PD=

1

2

PB
∵∠DCB=∠DAB，∠CPD=∠APB
∴△CPD∽△APB
∴

CD

AB

=

CP

AP

=

1

2

故答案为：

1

2

点评：本题考查三角形的相似，考查学生的计算能力，属于基础题．