题目内容
已知函数f（x）=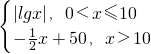
若a，b，c互不相等，且f（a）=f（b）=f（c），则lga+lgb+lgc的取值范围是________．
（1，2）
分析：画出函数的图象，根据f（a）=f（b）=f（c），不妨a＜b＜c，求出abc的范围即可．
解答：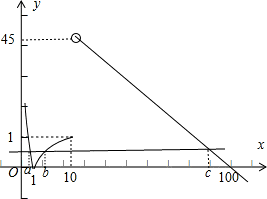
解：不妨设a＜b＜c，则由函数的解析式可得f（a）=f（b）=f（c），
即-lga=lgb=-
c+50∈（0，1），
∴ab=1，且0＜-c+50＜1，则abc=c∈（98，100），∴1＜lgc＜2，
故lga+lgb+lgc=lg（abc）=lgc∈（1，2）．
作出函数g（x）的图象如图：
故答案为（1，2）．
点评：本题主要考查分段函数、对数的运算性质以及利用数形结合解决问题的能力，属于基础题．
分析：画出函数的图象，根据f（a）=f（b）=f（c），不妨a＜b＜c，求出abc的范围即可．
解答：
解：不妨设a＜b＜c，则由函数的解析式可得f（a）=f（b）=f（c），即-lga=lgb=-
c+50∈（0，1），∴ab=1，且0＜-
c+50＜1，则abc=c∈（98，100），∴1＜lgc＜2，故lga+lgb+lgc=lg（abc）=lgc∈（1，2）．
作出函数g（x）的图象如图：
故答案为（1，2）．
点评：本题主要考查分段函数、对数的运算性质以及利用数形结合解决问题的能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列说法正确的是（ ）
| A、命题：“已知函数f（x），若f（x+1）与f（x-1）均为奇函数，则f（x）为奇函数，”为直命题 | B、“x＞1”是“|x|＞1”的必要不充分条件 | C、若“p且q”为假命题，则p，q均为假命题 | D、命题p：”?x∈R，使得x2+x+1＜0”，则?p：”?x∈R，均有x2+x+1≥0” |
，若f（a）=
，则实数a的值为（ ）
