题目内容
用与球心O距离为1的截面去截球,所得截面的面积为9p,则球的表面积为( ▲ )
| A.4p | B.10p | C.20p | D.40p |
D
分析:求出截面圆的半径,利用勾股定理求球的半径,然后求出球的表面积.
解:球的截面圆的半径为:9π=πr2,r=3
球的半径为: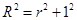
R=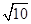
所以球的表面积:4πR2=4π×(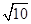 )2=40π
)2=40π
故选D.
点评:本题考查球的体积和表面积,考查计算能力,逻辑思维能力,是基础题
解:球的截面圆的半径为:9π=πr2,r=3
球的半径为:
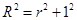
R=
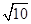
所以球的表面积:4πR2=4π×(
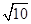 )2=40π
)2=40π故选D.
点评:本题考查球的体积和表面积,考查计算能力,逻辑思维能力,是基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
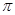
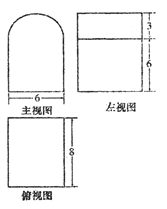
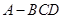 中,
中,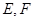 分别是
分别是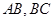 的中点,
的中点,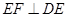 ,且
,且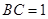 ,则正三棱锥
,则正三棱锥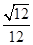
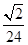
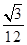
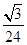
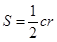 。类比这个结论,在空间中,果已知一个凸多面体有内切球,且内切球半径为R,那么凸多面体的体积V、表面积S'与内切球半径R之间的关系是
。类比这个结论,在空间中,果已知一个凸多面体有内切球,且内切球半径为R,那么凸多面体的体积V、表面积S'与内切球半径R之间的关系是 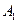 点,且
点,且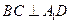 ;
;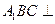 平面
平面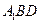 ;
;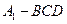 的体积.
的体积. 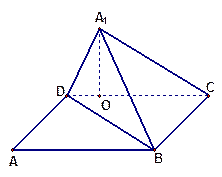
 是边长为
是边长为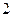 的等边三角形,
的等边三角形, 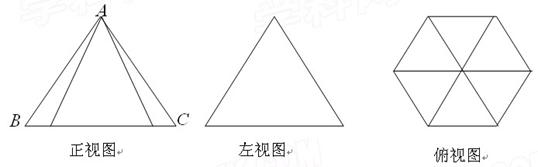
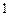 的正方体的外接球的表面积为 ▲ .
的正方体的外接球的表面积为 ▲ .