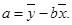题目内容
某市为节约用水,计划在本市试行居民生活用水定额管理,为了较为合理地确定居民日常用水量的标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),右表是100位居民月均用水量的频率分布表,根据右表解答下列问题:
| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.10 |
| [1,2) |  | 0.20 |
| [2,3) | 30 | 0.30 |
| [3,4) | 20 | 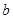 |
| [4,5) | 10 | 0.10 |
| [5,6] | 10 | 0.10 |
| 合计 | 100 | 1.00 |

(1)求右表中
 和
和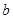 的值;
的值;(2)请将频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
(1) =20;
=20; 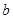 =0.20
=0.20
(2)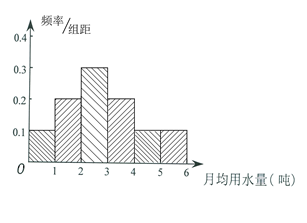
众数为2.5
解析试题分析:解:(1)根据频数为100,那么累加可知30+20+10+10+10+a=100 得到 =20; 2分
=20; 2分
在根据频率和为1,可知0.10+0.20+0.30+0.10+0.10+b=1,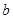 =0.20. 4分
=0.20. 4分
(2) 
根据直方图估计该市每位居民月均用水量的众数为2.5 8分
(说明:第二问中补充直方图与求众数只要做对一个得2分,两个全对的4分.)
考点:直方图
点评:主要是考查了频数表和直方图的运用,属于基础题。

 天天向上口算本系列答案
天天向上口算本系列答案某校高三期末统一测试,随机抽取一部分学生的数学成绩分组统计如下表:
(Ⅰ)求出表中 、
、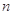 、
、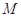 、
、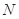 的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图;
| 分组 | 频数 | 频率 |
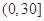 | 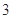 | 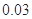 |
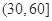 | 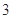 | 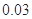 |
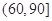 | 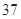 | 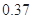 |
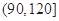 |  | 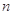 |
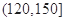 | 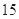 | 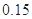 |
| 合计 | 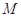 | 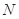 |

(Ⅱ)若全校参加本次考试的学生有600人,试估计这次测试中全校成绩在
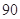 分以上的人数;
分以上的人数;(Ⅲ)若该校教师拟从分数不超过60的学生中选取2人进行个案分析,求被选中2人分数不超过30分的概率.
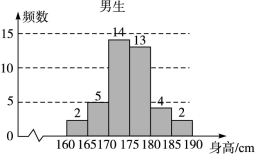
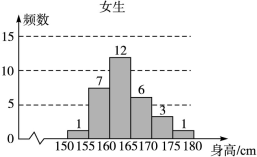
某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有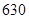 名学生,男女生人数之比为
名学生,男女生人数之比为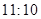 ,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为
,现按分层抽样方法抽取若干名学生,每人被抽到的概率均为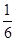 .
.
(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下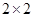 列联表:
列联表:
| | 否定 | 肯定 | 总计 |
| 男生 | | 10 | |
| 女生 | 30 | | |
| 总计 | | | |
②能否有
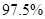 的把握认为态度与性别有关?
的把握认为态度与性别有关?(3)若一班有
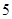 名男生被抽到,其中
名男生被抽到,其中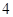 人持否定态度,
人持否定态度, 人持肯定态度;二班有
人持肯定态度;二班有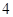 名女生被抽到,其中
名女生被抽到,其中 人持否定态度,
人持否定态度, 人持肯定态度.
人持肯定态度.现从这
 人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.
人中随机抽取一男一女进一步询问所持态度的原因,求其中恰有一人持肯定态度一人持否定态度的概率.解答时可参考下面临界值表:
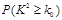 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
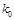 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
某校的研究性学习小组为了研究高中学生的身体发育状况,在该校随机抽出120名17至18周岁的男生,其中偏重的有60人,不偏重的也有60人。在偏重的60人中偏高的有40人,不偏高的有20人;在不偏重的60人中偏高和不偏高人数各占一半
(1)根据以上数据建立一个 列联表:
列联表:
| | 偏重 | 不偏重 | 合计 |
| 偏高 | | | |
| 不偏高 | | | |
| 合计 | | | |
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路 ”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
| | 男性 | 女性 | 合计 |
| 反感 | 10 | | |
| 不反感 | | 8 | |
| 合计 | | | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路 ”的路人的概率是
 .
.(Ⅰ)请将上面的列表补充完整(在答题卡上直接填写结果,不需要写求解过程),并据此资料分析反感“中国式过马路 ”与性别是否有关?(

当
 <2.706时,没有充分的证据判定变量性别有关,当
<2.706时,没有充分的证据判定变量性别有关,当
 >2.706时,有90%的把握判定变量性别有关,当
>2.706时,有90%的把握判定变量性别有关,当 >3.841时,有95%的把握判定变量性别有关,当
>3.841时,有95%的把握判定变量性别有关,当
 >6.635时,有99%的把握判定变量性别有关)
>6.635时,有99%的把握判定变量性别有关)(Ⅱ)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.附:
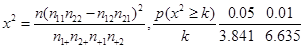
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
| | 患色盲 | 不患色盲 | 总计 |
| 男 | | 442 | |
| 女 | 6 | | |
| 总计 | 44 | 956 | 1000 |
随机变量

附临界值参考表:
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某设备的使用年限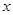 与所支出的总费用
与所支出的总费用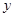 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限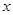 | 1 | 2 | 3 | 4 |
总费用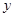 | 1.5 | 2 | 3 | 3.5 |

(Ⅱ)求出
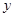 关于
关于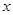 的线性回归方程
的线性回归方程 ;
;(III)当使用10年时,所支出的总费用约为多少万元。
参考公式:回归方程为
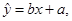 其中
其中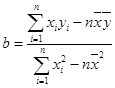 ,
,