题目内容
已知函数f(x)=ax2-2ax+2+b(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-mx在[2,4]上单调,求m的取值范围.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-mx在[2,4]上单调,求m的取值范围.
(1) (2)(-∞,2]∪[6,+∞)
(2)(-∞,2]∪[6,+∞)
 (2)(-∞,2]∪[6,+∞)
(2)(-∞,2]∪[6,+∞)解:(1)f(x)=a(x-1)2+2+b-a.
当a>0时,f(x)在[2,3]上为增函数,
故 ,⇒
,⇒
 ⇒
⇒
当a<0时,f(x)在[2,3]上为减函数,
故 ⇒
⇒
 ⇒
⇒
(2)∵b<1,∴a=1,b=0,
即f(x)=x2-2x+2.
g(x)=x2-2x+2-mx
=x2-(2+m)x+2,
∵g(x)在[2,4]上单调,
∴ ≤2或
≤2或 ≥4.
≥4.
∴m≤2或m≥6.
故m的取值范围为(-∞,2]∪[6,+∞).
当a>0时,f(x)在[2,3]上为增函数,
故
 ,⇒
,⇒ ⇒
⇒
当a<0时,f(x)在[2,3]上为减函数,
故
 ⇒
⇒ ⇒
⇒
(2)∵b<1,∴a=1,b=0,
即f(x)=x2-2x+2.
g(x)=x2-2x+2-mx
=x2-(2+m)x+2,
∵g(x)在[2,4]上单调,
∴
 ≤2或
≤2或 ≥4.
≥4.∴m≤2或m≥6.
故m的取值范围为(-∞,2]∪[6,+∞).

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 与加工时间
与加工时间 (单位:分钟)满足的函数关系
(单位:分钟)满足的函数关系 (
( 、
、 、
、 是常数),下图记录了三次实
是常数),下图记录了三次实 分钟
分钟  分钟
分钟 分钟
分钟 分钟
分钟
 ,则不等式f(x)>f(1)的解集是( )
,则不等式f(x)>f(1)的解集是( ) 上两个不同点处的切线重合,则称这条切线为曲线
上两个不同点处的切线重合,则称这条切线为曲线 ;②
;②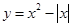 ;③
;③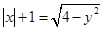 ;④
;④ 对应的曲线中存在“自公切线”的有( )
对应的曲线中存在“自公切线”的有( ) x ②f:x→y=
x ②f:x→y= x ③f:x→y=
x ③f:x→y= x ④f:x→y=x
x ④f:x→y=x 的定义域为
的定义域为 ,若函数
,若函数 ,使
,使 上的值域是
上的值域是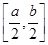 则称
则称 为“倍缩函数”,则的范围是( )
为“倍缩函数”,则的范围是( ) B.
B.
 D.
D.
 (x)=-x(x+1),则函数g(x)=f(logax)(0<a<1)的单调递减区间是( )
(x)=-x(x+1),则函数g(x)=f(logax)(0<a<1)的单调递减区间是( ) ,+∞),(0,1]
,+∞),(0,1]