Question

（2012•马鞍山二模）如图，已知椭圆的中心在原点，焦点在x轴上，长轴长是短轴长的2倍且经过点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），直线l交椭圆于A、B两个不同点（A、B与M不重合）．
（Ⅰ）求椭圆的方程；
（Ⅱ）当MA⊥MB时，求m的值．

Answer 1

分析：（Ⅰ）设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，根据长轴长是短轴长的2倍且经过点M（2，1），建立方程组，即可求得椭圆的方程；
（Ⅱ）依题意kOM=

1

2

，设直线l的方程代入椭圆方程，整理并利用韦达定理，结合MA⊥MB，即

MA

•

MB

=0，从而可求m的值．

解答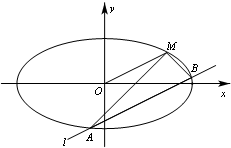：解：（Ⅰ）设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，
则

a=2b 4 a2 + 1 b2 =1

，∴a²=8，b²=2
∴椭圆方程为

x2

8

+

y2

2

=1…（6分）
（Ⅱ）依题意kOM=

1

2

，…（7分）
可设直线l的方程为：y=

1

2

x+m，A（x₁，y₁），B（x₂，y₂），则

MA

=(x1-2，y1-1)，

MB

=(x2-2，y2-1)
∵MA⊥MB，∴

MA

•

MB

=0，
∴x₁x₂-2（x₁+x₂）+y₁y₂-（y₁+y₂）+5=0
∴

5

4

x₁x₂+（

1

2

m-

5

2

）（x₁+x₂）+m²-2m+5=0…①
由y=

1

2

x+m代入椭圆方程，消y并整理化简得：x²+2mx+2m²-4=0
∴△=（2m）²-4（2m²-4）＞0，解得：-2＜m＜2…（10分）
由韦达定理得：x₁+x₂=-2m，x₁x₂=2m²-4代入①得：

5

4

（2m²-4）+（

1

2

m-

5

2

）×（-2m）+m²-2m+5=0…①
解得m=0或m=-

6

5

…（12分）
∵点A，B异于M，∴m=-

6

5

…（13分）

点评：本题考查椭圆的性质及直线和圆锥曲线的位置关系，考查向量知识的运用，属于中等题．