题目内容
若函数f(x)=ax+ka-x(a>0且a≠1)在R上既是奇函数,又是减函数,则g(x)=loga(x-k)的图象是( )
A、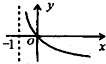 |
B、 |
C、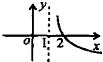 |
D、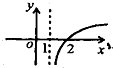 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:由f(x)为奇函数可得f(0)=0,由此求得k的值.再根据f(x)的单调性求得a的范围,可得g(x)的解析式.再根据对数函数的图象特征,得出结论.
解答:
解:由函数f(x)=ax+ka-x(a>0且a≠1)在R上是奇函数,
可得f(0)=0,即 1+k=0,解得 k=-1,故f(x)=ax-a-x.
再由f(x)是减函数,可得函数y=ax是减函数,故0<a<1.
g(x)=loga(x-k)=loga(x-1)的图象,是把函数y=logax的图象向右平移1个单位得到的,
故选A.
可得f(0)=0,即 1+k=0,解得 k=-1,故f(x)=ax-a-x.
再由f(x)是减函数,可得函数y=ax是减函数,故0<a<1.
g(x)=loga(x-k)=loga(x-1)的图象,是把函数y=logax的图象向右平移1个单位得到的,
故选A.
点评:本题主要考查函数的奇偶性和单调性的应用,对数函数的图象特征,函数图象的平移规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知tan(α-β)=
,tan(α+β)=
,则tan2α的值是( )
| 2 |
| 5 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若关于x的方程
=m-x有两个不等的实根,则m的取值范围是( )
| -x2-2x |
A、(-
| ||||
B、(-2,
| ||||
C、(0,
| ||||
D、[0,
|
使不等式23x-1>1成立的x的取值为( )
A、(
| ||
| B、(1,+∞) | ||
C、(
| ||
D、(-
|
若tanx=2则cos2x=( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
设全集U={x∈N*|x<6},集合A={1,3},∁UB={3,5},则A∩B=( )
| A、{1} | B、{1,5} |
| C、{4} | D、{2} |
设a、b∈R,已知命题p:a2+b2≤2ab,命题q:(
)2≤
,p是q成立的( )
| a+b |
| 2 |
| a2+b2 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |