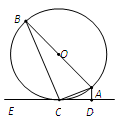题目内容
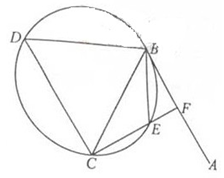
如图,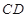 为△
为△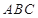 外接圆的切线,
外接圆的切线,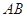 的延长线交直线
的延长线交直线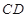 于点
于点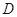 ,
,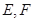 分别为弦
分别为弦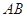 与弦
与弦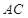 上的点,且
上的点,且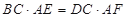 ,
,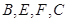 四点共圆.
四点共圆.
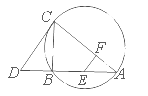
(Ⅰ)证明: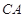 是△
是△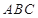 外接圆的直径;
外接圆的直径;
(Ⅱ)若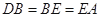 ,求过
,求过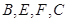 四点的圆的面积与△
四点的圆的面积与△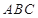 外接圆面积的比值.
外接圆面积的比值.
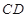 为△
为△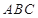 外接圆的切线,
外接圆的切线,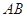 的延长线交直线
的延长线交直线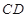 于点
于点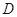 ,
,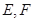 分别为弦
分别为弦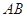 与弦
与弦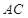 上的点,且
上的点,且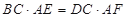 ,
,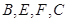 四点共圆.
四点共圆. 
(Ⅰ)证明:
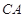 是△
是△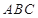 外接圆的直径;
外接圆的直径;(Ⅱ)若
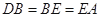 ,求过
,求过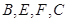 四点的圆的面积与△
四点的圆的面积与△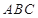 外接圆面积的比值.
外接圆面积的比值.(I)见解析;(II)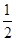 .
.
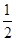 .
.试题分析:(I)证明
 是△
是△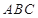 外接圆的直径,关键是证明
外接圆的直径,关键是证明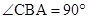 ,利用已知条件易于得到
,利用已知条件易于得到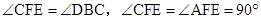 ;在利用
;在利用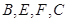 四点共圆,其对角互补即得证.
四点共圆,其对角互补即得证. (II)通过连接
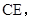 明确
明确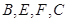 四点的圆的直径为
四点的圆的直径为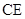 ,得到
,得到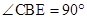 ;根据
;根据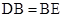 ,得
,得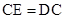 ,从而将圆面积之比,转化成
,从而将圆面积之比,转化成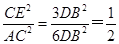 .
.试题解析:(I)证明:∵
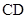 为△
为△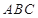 外接圆的切线,∴
外接圆的切线,∴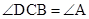 ,
,∵
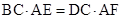 ,∴
,∴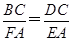 .
.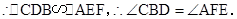
∵
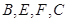 四点共圆,
四点共圆,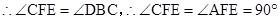 .
.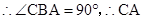 是△
是△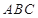 外接圆的直径;
外接圆的直径;(II)连接
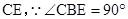 ,
,∴过
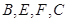 四点的圆的直径为
四点的圆的直径为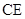 ,由
,由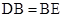 ,得
,得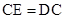 ,
,又
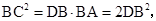
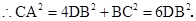
而
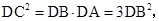
故过
 四点的圆的面积与△
四点的圆的面积与△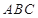 外接圆面积的比值为,
外接圆面积的比值为,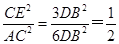 .
.
练习册系列答案
相关题目
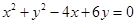 的圆心坐标是( )
的圆心坐标是( )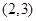
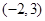
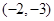
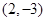
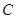 :
: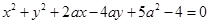 的圆心在第二象限内,则实数
的圆心在第二象限内,则实数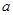 的取值范围为( )
的取值范围为( )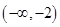

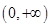
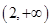
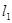 和
和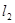 是平面内互相垂直的两条直线,它们的交点为
是平面内互相垂直的两条直线,它们的交点为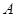 ,动点
,动点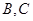 分别在
分别在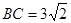 ,则过
,则过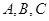 三点的动圆扫过的区域的面积为_____.
三点的动圆扫过的区域的面积为_____.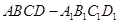 的棱长为2,点
的棱长为2,点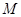 是
是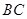 的中点,点
的中点,点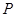 是正方形
是正方形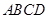 所在平面内的一个动点,且满足
所在平面内的一个动点,且满足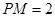 ,
,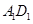 的距离为
的距离为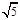 ,则点
,则点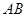 为圆的切线,切点为
为圆的切线,切点为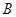 ,点
,点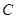 在圆上,
在圆上,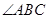 的角平分线
的角平分线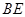 交圆于点
交圆于点 ,
, 垂直
垂直 。
。
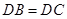 ;
;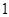 ,
,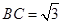 ,延长
,延长 交
交 ,求
,求 外接圆的半径。
外接圆的半径。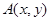 实施变换
实施变换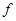 后,对应点为
后,对应点为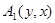 ,给出以下命题:
,给出以下命题: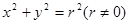 上任意一点实施变换
上任意一点实施变换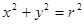 ;
;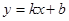 上每一点实施变换
上每一点实施变换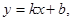 则
则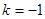 ;
;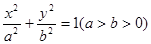 上每一点实施变换
上每一点实施变换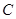 :
: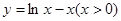 上每一点实施变换
上每一点实施变换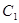 ,
,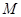 是曲线
是曲线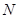 是曲线
是曲线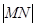 的最小值为
的最小值为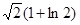 。
。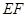 的长度为1,端点
的长度为1,端点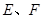 在边长为2的正方形
在边长为2的正方形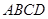 的四边上滑动.当
的四边上滑动.当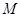 所形成的轨迹为
所形成的轨迹为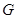 ,若
,若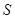 ,则
,则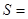 .
.
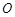 的直径
的直径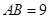 ,直线
,直线 与圆
与圆 相切于点
相切于点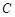 ,
,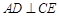 于
于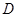 ,若
,若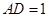 ,设
,设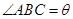 ,则
,则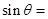 ______.
______.