题目内容
|
(本小题共13分) 在平面直角坐标系中,已知圆的圆心为,过点且斜率为的直线与圆相交于不同的两点. (Ⅰ)求圆的面积; (Ⅱ)求的取值范围; (Ⅲ)是否存在常数,使得向量与共线?如果存在,求的值;如果不存在,请说明理由. (本小题共13分) 解:(Ⅰ)圆的方程可化为 故圆的面积为 (Ⅱ)设直线 法一: 将直线方程代入圆方程得 整理得 直线与圆交于两个不同的点
解得 法二: 直线
化简得 解得 (Ⅲ)设
又 而 所以 将②③代入上式,解得 由(Ⅱ)知 
练习册系列答案
相关题目
北京市房山区2011年高三上学期期末统练试卷(数学理).doc | | |
|
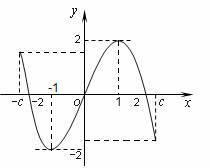 ②函数是奇函数的充要条件是;
②函数是奇函数的充要条件是;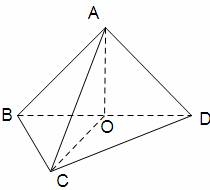 (II)求证:;
(II)求证:;