题目内容
数列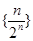 的前
的前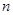 项的和为
项的和为
A.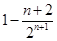 | B.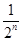 |
C.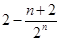 | D.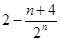 |
C
解析试题分析: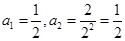 。故
。故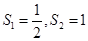 。当
。当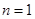 时,
时,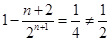 ,排除A;
,排除A;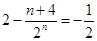 ,排除D。当
,排除D。当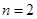 时,
时,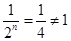 ,排除B。选C。
,排除B。选C。
考点:本题主要考查“特值法”(或错位相减法)。
点评:错位相减法是求“差比积”数列前n项和的基本方法,是高考考查重点之一。对选择题,则不拘泥于常规,利用“特值法”反映解题的灵活性。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列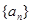 的前
的前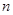 项和为
项和为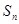 ,且
,且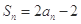 则
则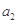 等于( )
等于( )
| A.4 | B.2 | C.1 | D.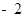 |
已知数列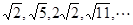 ,则
,则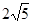 是这个数列的 ( )
是这个数列的 ( )
A.第 项 项 | B.第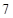 项 项 | C.第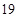 项 项 | D.第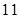 项 项 |
在各项均为正数的数列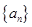 中,对任意
中,对任意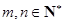 都有
都有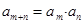 .若
.若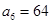 ,
,
则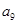 等于( )
等于( )
| A.256 | B.510 | C.512 | D.1024 |
下列四个数中,哪一个是数列{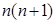 }中的一项( )
}中的一项( )
| A.380 | B.39 | C.35 | D. 23 |
数列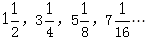 的前
的前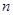 项和为 ( )
项和为 ( )
A.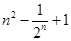 | B.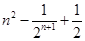 |
C.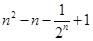 | D.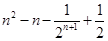 |
已知数列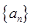 满足
满足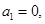
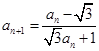 ,则
,则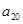 =( )
=( )
A. | B.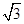 | C.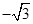 | D. |
、数列{an}、{bn}的通项公式分别是an="an+b" (a≠0,a、b∈R),bn=qn-1(q>1),则数列{an}、{bn}中,使an=bn的n值的个数是( )
| A.2 | B.1 |
| C.0 | D.可能为0,可能为1,可能为2 |
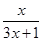 ,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.
,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.