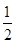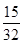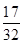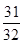题目内容
箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为 ( )
A. | B.( )3× )3× | C. × × | D. ×( ×( )3× )3× |
B
解析试题分析:从箱子里每次随机取出一个球为黑球的概率为 ,从箱子里每次随机取出一个球为黑球的概率为
,从箱子里每次随机取出一个球为黑球的概率为 。根据题意,前4次必须为黑球,第5 次为白球,∴第4次取球之后停止的概率为(
。根据题意,前4次必须为黑球,第5 次为白球,∴第4次取球之后停止的概率为( )3×
)3× ,故选B
,故选B
考点:本题考查了独立事件概率的求法
点评:对于相互独立事件同时发生的概率问题,其求解的一般步骤是:①确定众事件是相互独立的;②确定众事件会同时发生;③先求每个事件发生的概率,再求它们的积。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,那么互斥不对立的两个事件是
| A.恰有1名男生与恰有2名女生 |
| B.至少有1名男生与全是男生 |
| C.至少有1名男生与至少有1名女生 |
| D.至少有1名男生与全是女生 |
某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽验一只是正品(甲级)的概率为( )
| A.0.95 | B.0.97 | C.0.92 | D.0.08 |
从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,那么互斥而不对立的两个事件是
个球,那么互斥而不对立的两个事件是
| A.至少有一个黒球与都是红球 | B.至少有一个黒球与都是黒球 |
C.至少有一个黒球与至少有 个红球 个红球 | D.恰有 个黒球与恰有 个黒球与恰有 个黒球 个黒球 |
已知随机变量X服从正态分布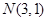 ,且
,且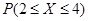 =0.6826,则
=0.6826,则 =( )
=( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.1585 |
设随机变量X~ ,则P(X=3)的值是( )
,则P(X=3)的值是( )
A. | B. | C. | D. |
下列说法正确的是
| A.互斥事件一定是对立事件,对立事件不一定是互斥事件 |
| B.互斥事件不一定是对立事件,对立事件一定是互斥事件 |
C.事件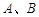 中至少有一个发生的概率一定比 中至少有一个发生的概率一定比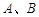 中恰有一个发生的概率大 中恰有一个发生的概率大 |
D.事件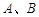 同时发生的概率一定比 同时发生的概率一定比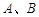 中恰有一个发生的概率小 中恰有一个发生的概率小 |
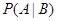 为( )
为( )
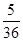
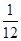
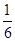
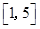 和
和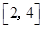 分别取一个数,记为
分别取一个数,记为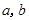 , 则方程
, 则方程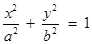 表示焦点在
表示焦点在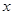 轴上且离心率小于
轴上且离心率小于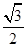 的椭圆的概率为
的椭圆的概率为