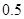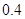题目内容
某产品分甲、乙、丙三级,其中乙、丙两级均属次品,在正常生产情况下,出现乙级品和丙级品的概率分别是5%和3%,则抽验一只是正品(甲级)的概率为( )
| A.0.95 | B.0.97 | C.0.92 | D.0.08 |
C
解析试题分析:记抽验的产品是甲级品为事件A,是乙级品为事件B,是丙级品为事件C,这三个事件彼此互斥,因而抽验产品是正品(甲级)的概率为P(A)=1-P(B)-P(C)=1-5%-3%=92%=0.92.
考点:本题考查了互斥事件的概率的求解
点评:弄清事件的类型,选择相应的概率公式是解决此类问题的关键,属基础题

练习册系列答案
相关题目
某射击运动员射击所得环数ξ的分布列如下所示,则P(ξ=8)=( )
| ξ | 7 | 8 | 9 | 10 |
| P | 0.21 | m | 0.29 | 0.22 |
下列叙述正确的是
A.任何事件的概率总是在 之间 之间 |
| B.频率是客观存在的,与试验次数无关 |
| C.随着试验次数的增加,频率一般会越来越接近概率 |
| D.概率是随机的,在试验前不能确定 |
从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )
| A.至少有一个红球与都是红球 |
| B.至少有一个红球与都是白球 |
| C.至少有一个红球与至少有一个白球 |
| D.恰有一个红球与恰有二个红球 |
箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为 ( )
A. | B.( )3× )3× | C. × × | D. ×( ×( )3× )3× |
已知随机变量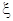 服从正态分布
服从正态分布 且
且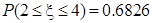 ,则
,则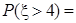 ( )
( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.1585 |
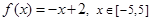 .若从区间
.若从区间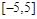 内随机选取一个实数
内随机选取一个实数 ,则所选取的实数
,则所选取的实数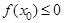 的概率为 ( )
的概率为 ( )