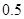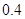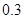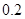题目内容
抛掷红、蓝两个骰子,事件A=“红骰子出现4点”,事件B=“蓝骰子出现的点数是偶数”,则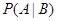 为( )
为( )
A. | B.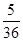 | C.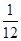 | D.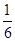 |
D
解析试题分析:先分别计算PP(B),P(AB),再利用条件概率公式P(A|B)=P(AB):P(B),即可求得概率.解:由题意,基本事件空间中的事件数为n(Ω)=36(个),n(B)=3×6=18(个),则可知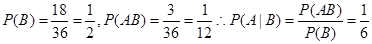 ,故可知答案为D.
,故可知答案为D.
考点:条件概率
点评:本题以条件概率为载体,考查条件概率的计算,解题的关键是判断概率的类型,从而利用相应公式

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
下图是正态分布N(0,1)的正态曲线图,下面3个式子中,等于图中阴影部分面积的个数为( )。注:Φ P
P

① ②
② ③
③
| A.0 | B.1 | C.2 | D.3 |
从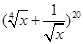 的展开式中任取一项,则取到有理项的概率为( )
的展开式中任取一项,则取到有理项的概率为( )
A.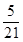 | B.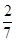 | C.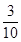 | D.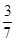 |
若在区域 内任取一点P,则点P恰好在单位圆
内任取一点P,则点P恰好在单位圆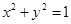 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
下列叙述正确的是
A.任何事件的概率总是在 之间 之间 |
| B.频率是客观存在的,与试验次数无关 |
| C.随着试验次数的增加,频率一般会越来越接近概率 |
| D.概率是随机的,在试验前不能确定 |
箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为 ( )
A. | B.( )3× )3× | C. × × | D. ×( ×( )3× )3× |
设A,B是任意事件,下列哪一个关系式正确的( )
| A.A+B=A | B.AB A A | C.A+AB=A | D.  A A |
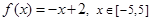 .若从区间
.若从区间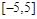 内随机选取一个实数
内随机选取一个实数 ,则所选取的实数
,则所选取的实数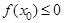 的概率为 ( )
的概率为 ( )