题目内容
从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,那么互斥而不对立的两个事件是
个球,那么互斥而不对立的两个事件是
| A.至少有一个黒球与都是红球 | B.至少有一个黒球与都是黒球 |
C.至少有一个黒球与至少有 个红球 个红球 | D.恰有 个黒球与恰有 个黒球与恰有 个黒球 个黒球 |
D
解析试题分析:选项A中的两个事件是对立事件,选项B中的两个事件既不互斥也不对立,选项C中的两个事件既不互斥也不对立,故选D
考点:本题考查了互斥事件、对立事件的概念
点评:正确理解互斥事件与对立事件的区别与联系是解决此类问题的关键,属基础题

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
在区间 上任取2个数
上任取2个数 ,若向量
,若向量 ,则
,则 的概率是
的概率是
A. | B.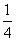 |
C. | D. |
若在区域 内任取一点P,则点P恰好在单位圆
内任取一点P,则点P恰好在单位圆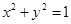 内的概率为( )
内的概率为( )
A. | B. | C. | D. |
将一枚质地均匀的硬币连掷4次,出现“至少两次正面向上”的概率为
A. | B. | C. | D. |
箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为 ( )
A. | B.( )3× )3× | C. × × | D. ×( ×( )3× )3× |
下列说法正确的个数是
(1)线性回归方程 必过
必过
(2)在一个 列联表中,由计算得
列联表中,由计算得 =4.235,则有95%的把握确认这两个变量间没有关系
=4.235,则有95%的把握确认这两个变量间没有关系
(3)复数
(4)若随机变量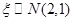 ,且p(
,且p( <4)=p,则p(0<
<4)=p,则p(0< <2)=2p-1
<2)=2p-1
| A.1 | B.2 | C.3 | D. 4 |
已知函数 ,其中
,其中 ,则使得
,则使得 在
在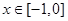 上有解的概率为( )
上有解的概率为( )
A. | B. | C.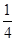 | D. |
一个均匀正方体玩具的各个面上分别标有数字1,2,3,4,5,6.将这个玩具向上抛掷1次,设事件A表示向上的一面出现奇数点,事件B表示向上的一面出现的点数不超过3,事件C表示向上的一面出现的点数不小于4,则( )
| A.A与B是互斥而非对立事件 | B.A与B是对立事件 |
| C.B与C是互斥而非对立事件 | D.B与C是对立事件 |



