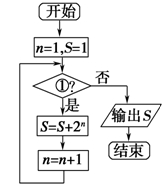
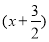题目内容
在直角坐标系xOy中,椭圆C的参数方程为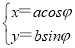 (φ为参数,a>b>0),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为ρsin(θ+
(φ为参数,a>b>0),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为ρsin(θ+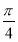 )=
)=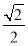 m(m为非零数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,求椭圆C的离心率.
m(m为非零数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,求椭圆C的离心率.
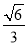
【解析】椭圆C的标准方程为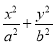 =1(a>b>0),
=1(a>b>0),
由ρsin(θ+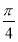 )=
)= m,得ρsin θ+ρcos θ=m,
m,得ρsin θ+ρcos θ=m,
∴直线l的普通方程为x+y=m,又圆ρ=b的普通方程为x2+y2=b2(b>0),
不妨设直线l过椭圆C的右焦点F2(c,0),则c=m,又直线l与圆x2+y2=b2相切,
∴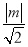 =b,因此c=
=b,因此c=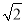 b,即c2=2(a2-c2),
b,即c2=2(a2-c2),
∴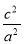 =
=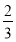 ,故椭圆C的离心率e=
,故椭圆C的离心率e=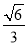

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| 专业A | 专业B | 总计 |
女生 | 12 | 4 | 16 |
男生 | 38 | 46 | 84 |
总计 | 50 | 50 | 100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=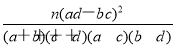
P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |