题目内容
命题“若
，则
是直角三角形”的逆命题、否命题、逆否命题这三个命题中，真命题的个数是（ ）
| A．0 | B．1 | C．2 | D．3 |
B
解析试题分析：因为原命题“若，则是直角三角形”是真命题，由互为逆否命题的两个命题的真假性相同可知它的逆否命题也是真命题；而逆命题为“若是直角三角形，则”，这是假命题，因为是直角三角形时，内角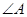
、
、
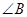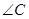中有一个是直角即可，所以不一定是，由逆命题与否命题是互为逆否命题的关系，所以否命题也是假命题，故在逆命题、否命题、逆否命题这三个命题中真命题的个数只有一个，选B.
考点：1.命题真假的判断；2.四种命题及其关系.
练习册系列答案
相关题目
已知不重合的两直线
与
对应的斜率分别为
与
，则“
”是“∥”的（ ）
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不是充分也不是必要条件 |
已知
，
，则
是
成立的 ( )
| A．必要不充分条件 | B．充分不必要条件 |
| C．充要条件 | D．既不充分也不必要条件 |
命题“所有自然数的平方都是正数”的否定为 ( )
| A．所有自然数的平方都不是正数 |
| B．有的自然数的平方是正数 |
| C．至少有一个自然数的平方是正数 |
| D．至少有一个自然数的平方不是正数 |
对于命题p:?x∈[0,+∞),(log32)x≤1,( )
A．是假命题, p:?x0∈[0,+∞), >1 |
| B．是假命题,p:?x∈[0,+∞),(log32)x≥1 |
| C．是真命题,p:?x0∈[0,+∞), >1 |
| D．是真命题,p:?x∈[0,+∞),(log32)x≥1 |
下面四个条件中,使a>b成立的充分而不必要条件是( )
| A．a>b+1 | B．a>b-1 | C．a2>b2 | D．a3>b3 |
已知函数f(x)＝Acos(ωx＋φ)(A>0，ω>0，φ∈R)，则“f(x)是奇函数”是“φ＝
”的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充分必要条件 | D．既不充分也不必要条件 |
已知集合A，B，则A∪B＝A是A∩B＝B的( )
| A．充分不必要条件 | B．必要不充分条件 | C．充要条件 | D．既不充分也不必要条件 |
已知直线l⊥平面α，直线m∥平面β，则“α∥β”是“l⊥m”的( )．
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |